
【题目】小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.
(1)求点A到地面的距离AG;
(2)求A,B之间的距离.(结果精确到0.1m)(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
【答案】
(1)
由已知得:∠AGD=∠BGE=∠CFD=90°,∠CDF=α=45°,
∴DF=CF=10,DG=FG+FD=15+10=25,
∴AG=GD=25,
答:位置A离地面的垂直距离为25米.
(2)
∵∠CEF=β=35°,
∴ ![]() tan∠CEF=tan35°≈0.70,
tan∠CEF=tan35°≈0.70,
∴EF= ![]()
![]() ≈14.29,
≈14.29,
∴EG=GF+EF=15+14.29=29.29,
又∵ ![]() tan∠CEF=tan35°≈0.70,
tan∠CEF=tan35°≈0.70,
∴BG=0.70EG=0.70×29.29≈20.50,
∴AB≈25-20.50≈4.5.
答:A,B相差4.5米.
【解析】(1)因为∠AGD=∠BGE=∠CFD=90°,∠CDF=α=45°,,根据等腰直角三角形的性质,易得AG=GD=FG+FD= FG+CF;(2)因为∠CEF=β=35°,所以 ![]()
![]() tan∠CEF , CF已知,可先求出EF,则可得EG,BG,由AB=AG-BG可解得.
tan∠CEF , CF已知,可先求出EF,则可得EG,BG,由AB=AG-BG可解得.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】在4张完全相同的卡片正面分别写上数字1,2,3,3,现将它们的背面朝上洗均匀.
(1)随机抽出一张卡片,求抽到数字“3”的概率;
(2)若随机抽出一张卡片记下数字后放回并洗均匀,再随机抽出一张卡片,求两次都是抽到数字“3”的概率;(要求画树状图或列表求解)
(3)如果再增加若干张写有数字“3”的同样卡片,洗均匀后,使得随机抽出一张卡片是数字“3”的概率为 ![]() ,问增加了多少张卡片?
,问增加了多少张卡片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么当再过多长时间轮船离灯塔最近?( )
A.1小时
B.![]()
小时
C.2小时
D.2 ![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C的内接△AOB中,AB=AO=4,tan∠AOB= ![]() ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
(1)求抛物线的函数解析式;
(2)直线m与C相切于点A,交y轴于点D,求证:AD//OB;
(3)在(2)的条件下,点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒1个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABO的边长为2,O为坐标原点,A在 ![]() 轴上,B在第二象限。△ABO沿
轴上,B在第二象限。△ABO沿 ![]() 轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.
轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.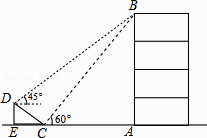
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com