
【题目】计算:|﹣3|+ ![]() tan30°﹣
tan30°﹣ ![]() ﹣(2017﹣π)0 .
﹣(2017﹣π)0 .
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.
(1)求点A到地面的距离AG;
(2)求A,B之间的距离.(结果精确到0.1m)(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
售价(元/台) | 月销售量(台) |
400 | 200 |
| 250 |
x |
|
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1 , A2 , A3 , …,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1 , A2 , A3 , …,An+1作x轴的垂线交一次函数 ![]() 的图象于点B1 , B2 , B3 , …,Bn+1 , 连接A1B2 , B1A2 , A2B3 , B2A3 , …,AnBn+1 , BnAn+1依次产生交点P1 , P2 , P3 , …,Pn , 则Pn的坐标是 .
的图象于点B1 , B2 , B3 , …,Bn+1 , 连接A1B2 , B1A2 , A2B3 , B2A3 , …,AnBn+1 , BnAn+1依次产生交点P1 , P2 , P3 , …,Pn , 则Pn的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC中,点D、E、F、分别为边AB,AC,BC的中点,M为直线BC动点,△DMN为等边三角形
(1)如图1,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?
(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立请说明理由;
(3)若点M在点C右侧时,请你在图3中画出相应的图形,并判断(1)的结论是否仍然成立?若成立,请直接写出结论,若不成立请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF. 
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF= ![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB⊥BD, ![]() =
= ![]() ,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线
,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线 ![]() (k>0)同时经过B、D两点,则点B的坐标是
(k>0)同时经过B、D两点,则点B的坐标是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 83 | 79 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4). 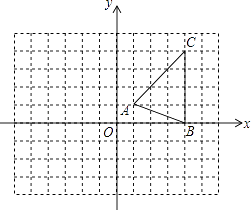
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2 .
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com