
【题目】如图,直线![]() 与x轴、y轴分别交于点B、C,对称轴为
与x轴、y轴分别交于点B、C,对称轴为![]() 的抛物线经过B、C两点,与x轴的另一个交点为A,顶点为D、点P是该抛物线上的一个动点,过点P作
的抛物线经过B、C两点,与x轴的另一个交点为A,顶点为D、点P是该抛物线上的一个动点,过点P作![]() 轴于点E,分别交线段BD、BC于点F、G,设点P的横坐标为
轴于点E,分别交线段BD、BC于点F、G,设点P的横坐标为![]() .
.
![]() 求该抛物线所对应的函数关系式及顶点D的坐标;
求该抛物线所对应的函数关系式及顶点D的坐标;
![]() 求证:
求证:![]() ;
;![]() ;
;
![]() 当
当![]() 为等腰三角形时,求t的值.
为等腰三角形时,求t的值.

【答案】![]()
![]() ,D坐标为
,D坐标为![]() ;
;![]() 证明见解析;
证明见解析;![]() 证明见解析;
证明见解析;![]() t的值为
t的值为![]() 或
或![]() .
.
【解析】
(1)由抛物线特点求出A的坐标,再用待定系数法求出函数解析式,再求顶点坐标;(2)![]() 求直线DB所对应的函数关系式为
求直线DB所对应的函数关系式为![]() .设点P的坐标为
.设点P的坐标为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 过点D作
过点D作![]() 轴,垂足为点H,由等腰直角三角形性质得
轴,垂足为点H,由等腰直角三角形性质得![]() ,
,![]() ,
,![]() ,所以,在
,所以,在![]() 中,
中,![]() ;在
;在![]() 中,
中,![]() .
.
![]() 分三种情况讨论:
分三种情况讨论:
![]() Ⅰ
Ⅰ![]() 若
若![]() 则
则![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 则
则![]() ;
;
![]() Ⅲ
Ⅲ![]() 若
若![]() 则
则![]() ;
;
分别解方程可得.
解:![]() 直线
直线![]() 与x轴、y轴的交点坐标分别为
与x轴、y轴的交点坐标分别为![]() ,
,![]() .
.
![]() 抛物线的对称轴为
抛物线的对称轴为![]() ,
,
![]() 点A坐标为
点A坐标为![]()
![]() 设所求抛物线的函数关系式为
设所求抛物线的函数关系式为![]() ,
,
把点![]() 代入,得
代入,得![]() ,
,
解得![]() .
.
![]() 所求抛物线的函数关系式为:
所求抛物线的函数关系式为:![]() ,即
,即![]() .
.
![]() 该抛物线的顶点D的坐标为
该抛物线的顶点D的坐标为![]() .
.
![]() ,
,![]() .
.
易得直线DB所对应的函数关系式为![]() .
.
设点P的坐标为![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ,即
,即![]() .
.
![]() 过点D作
过点D作![]() 轴,垂足为点H,如图.
轴,垂足为点H,如图.

![]() 点D、C的坐标分别为
点D、C的坐标分别为![]() 、
、![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
![]() 是直角三角形,且
是直角三角形,且![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
![]() .
.
![]() 分三种情况讨论:
分三种情况讨论:
![]() Ⅰ
Ⅰ![]() 若
若![]() 则
则![]() ,
,
整理得![]() ,
,
解得![]() ,
,![]() 舍去
舍去![]() .
.
![]() Ⅱ
Ⅱ![]() 若
若![]() 则
则![]() ,
,
整理得![]() ,
,
解得![]() ,
,![]() .
.
![]() ,
,
![]() 这种情况不存在.
这种情况不存在.
![]() Ⅲ
Ⅲ![]() 若
若![]() 则
则![]() ,
,
整理得![]() ,
,
解得![]() ,
,![]() .
.
![]() ,
,
![]() 不符合题意,舍去.
不符合题意,舍去.
综上所述,当![]() 为等腰三角形时,t的值为
为等腰三角形时,t的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y(m3)与放水时间t(分)有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | … |
水池中水量(m3) | 38 | 36 | 34 | 32 | … |
下列结论中正确的是( )
A. y随t的增加而增大
B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3
D. y与t之间的关系式为y=40t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 的AB边为直径作
的AB边为直径作![]() 交BC于点D,过点D作
交BC于点D,过点D作![]() 切线交AC于点E,
切线交AC于点E,![]() .
.
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,设CA的延长线交
如图2,设CA的延长线交![]() 于点F,点G在
于点F,点G在![]() 上,
上,![]() ,连接BG,求证:
,连接BG,求证:![]() ;
;
![]() 在
在![]() 的条件下,如图3,点M为BG中点,MD的延长线交CE于点N,连接DF交AB于点H,若AH:
的条件下,如图3,点M为BG中点,MD的延长线交CE于点N,连接DF交AB于点H,若AH:![]() :8,
:8,![]() ,求DE长.
,求DE长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家“一带一路”的倡议下,2018年6月将在浙江宁波举办中国![]() 中东欧国家投资贸易博览会,某东欧客商准备在宁波采购一批特色商品.
中东欧国家投资贸易博览会,某东欧客商准备在宁波采购一批特色商品.

![]() 根据以上信息,求一件A,B型商品的进价分别为多少元?
根据以上信息,求一件A,B型商品的进价分别为多少元?
![]() 若该东欧客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元
若该东欧客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元![]() 件,B型商品的售价为220元
件,B型商品的售价为220元![]() 件,且全部售出,设购进A型商品m件,写出该客商销售这批商品的利润与m之间的函数关系式,并求出利润的最大值.
件,且全部售出,设购进A型商品m件,写出该客商销售这批商品的利润与m之间的函数关系式,并求出利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.

证明:∵AB∥CD( ),
∴∠AEF=∠EFD( ),
∵EG平分∠AEF,FH平分∠EFD( ),
∴∠ =![]() ∠AEF,
∠AEF,
∠ =![]() ∠EFD(角平分线定义),
∠EFD(角平分线定义),
∴∠ =∠ .
∴EG∥FH( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
整式乘法与因式分解是方向相反的变形,由![]()
![]() ,
,
可得 ![]() .
.
利用这个式子可以将某些二次项系数是1的二次三项式分解因式.
例如:将式子![]() 分解因式.
分解因式.
这个式子的常数项![]() ,一次项系
,一次项系![]() ,
,
所以![]() .
.

解:![]()
![]() .
.
上述分解因式![]() 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如右图).
的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如右图).
请仿照上面的方法,解答下列问题:
(1)分解因式:![]() =___________________;
=___________________;
(2)若![]() 可分解为两个一次因式的积,则整数P的所有可能值是________.
可分解为两个一次因式的积,则整数P的所有可能值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )
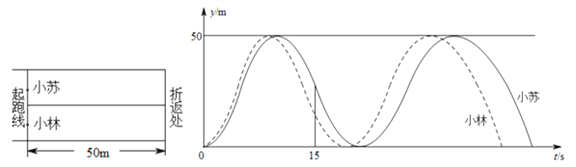
A. 两人从起跑线同时出发,同时到达终点.
B. 小苏跑全程的平均速度大于小林跑全程的平均速度.
C. 小苏在跑最后100m的过程中,与小林相遇2次.
D. 小苏前15s跑过的路程小于小林前15s跑过的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=![]() -5x+4 的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
-5x+4 的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
x | … |
|
| -2 |
|
| -1 |
|
| 0 |
|
| 1 |
|
| 2 |
| td style="width:17.7pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; border-bottom-style:solid; border-bottom-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">… | |
y | … | 4.3 | 3.2 | 0 | -2.2 | -1.4 | 0 | 2.8 | 3.7 | 4 | 3.7 | 2.8 | 0 | -1.4 | -2.2 | m | 3.2 | 4.3 | … |
其中m= ;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察函数图象,写出一条该函数的性质 ;
(4)进一步探究函数图象发现:
①方程![]() 有 个互不相等的实数根;
有 个互不相等的实数根;
②有两个点(x1,y1)和(x2,y2)在此函数图象上,当x2 >x1>2时,比较y1和y2的大小关系为:
y1 y2 (填“>”、“<”或“=”) ;
③若关于x的方程![]() 有4个互不相等的实数根,则a的取值范围是 .
有4个互不相等的实数根,则a的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )

A.∠A=∠C+∠E+∠FB.∠A+∠E-∠C-∠F=180°
C.∠A+∠C-∠E-∠F=180°D.∠A+∠E+∠C+∠F=360°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com