
【题目】已知:如图,AB∥CD,EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.

证明:∵AB∥CD( ),
∴∠AEF=∠EFD( ),
∵EG平分∠AEF,FH平分∠EFD( ),
∴∠ =![]() ∠AEF,
∠AEF,
∠ =![]() ∠EFD(角平分线定义),
∠EFD(角平分线定义),
∴∠ =∠ .
∴EG∥FH( )
【答案】已知,两直线平行,内错角相等;已知;GEF;HFE;GEF;HFE;内错角相等,两直线平行
【解析】
由AB与CD平行,利用两直线平行,内错角相等得到一对角相等,再由EG与FH为角平分线,利用角平分线定义及等量代换得到一对内错角相等,利用内错角相等两直线平行即可得证.
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(两直线平行,内错角相等).
∵EG平分∠AEF,FH平分∠EFD(已知).
∴∠GEF=![]() ∠AEF,∠HFE=
∠AEF,∠HFE=![]() ∠EFD,(角平分线定义)
∠EFD,(角平分线定义)
∴∠GEF=∠HFE,
∴EG∥FH(内错角相等,两直线平行).
故答案为:已知,两直线平行,内错角相等;已知;GEF;HFE;GEF;HFE;内错角相等,两直线平行


科目:初中数学 来源: 题型:
【题目】已知,![]() 是等边三角形,
是等边三角形,![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为顶点做
为顶点做![]() .
. ![]() 交过
交过![]() 且平行于
且平行于![]() 的直线于
的直线于![]() ,求证:
,求证:![]() ;当
;当![]() 为
为![]() 的中点时,(如图1)小明同学很快就证明了结论:他的做法是:取
的中点时,(如图1)小明同学很快就证明了结论:他的做法是:取![]() 的中点
的中点![]() ,连结
,连结![]() ,然后证明
,然后证明![]() . 从而得到
. 从而得到![]() ,我们继续来研究:
,我们继续来研究:
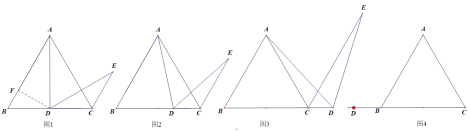
(1)如图2、当D是BC上的任意一点时,求证:![]()
(2)如图3、当D在BC的延长线上时,求证:![]()
(3)当![]() 在
在![]() 的延长线上时,请利用图4画出图形,并说明上面的结论是否成立(不必证明).
的延长线上时,请利用图4画出图形,并说明上面的结论是否成立(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠C=90°,∠BAC=60°,AB的垂直平分线DE交AB于D,交BC于E,若CE=3cm,则BE的长为( )

A.6cm B.5cm C.4cm D.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波城区中考体育选测项目进行了现场抽取,最终确定了宁波城区2018年体育选测项目:跳绳、篮球运动投篮、立定跳远,某中学随机抽取了一部分九年级女同学进行1分钟跳绳抽测,将测得的成绩绘制成如下的统计图表:

级别 | 成绩 | 频数 |
A |
| 2 |
B |
| 7 |
C |
| 14 |
D |
| 12 |
E |
|
![]() 本次随机抽取了______名九年级女同学;
本次随机抽取了______名九年级女同学;
![]() 频数分布表中,成绩是E级的频数是多少?
频数分布表中,成绩是E级的频数是多少?
![]() 若认定“D,E”两个级别的成绩为“优秀”,全校九年级女同学共有200人,请估计该校跳绳成绩优秀的女同学人数.
若认定“D,E”两个级别的成绩为“优秀”,全校九年级女同学共有200人,请估计该校跳绳成绩优秀的女同学人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 和
和![]() 的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数
的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数![]() 和
和![]() 互为中心对称函数.
互为中心对称函数.
![]() 求函数
求函数![]() 的中心对称函数;
的中心对称函数;
![]() 如图,在平面直角坐标系xOy中,E,F两点的坐标分别为
如图,在平面直角坐标系xOy中,E,F两点的坐标分别为![]() ,
,![]() ,二次函数
,二次函数![]() 的图象经过点E和原点O,顶点为
的图象经过点E和原点O,顶点为![]() 已知函数
已知函数![]() 和
和![]() 互为中心对称函数;
互为中心对称函数;
![]() 请在图中作出二次函数
请在图中作出二次函数![]() 的顶点
的顶点![]() 作图工具不限
作图工具不限![]() ,并画出函数
,并画出函数![]() 的大致图象;
的大致图象;
![]() 当四边形EPFQ是矩形时,请求出a的值;
当四边形EPFQ是矩形时,请求出a的值;
![]() 已知二次函数
已知二次函数![]() 和
和![]() 互为中心对称函数,且
互为中心对称函数,且![]() 的图象经过
的图象经过![]() 的顶点当
的顶点当![]() 时,求代数式
时,求代数式![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点B、C,对称轴为
与x轴、y轴分别交于点B、C,对称轴为![]() 的抛物线经过B、C两点,与x轴的另一个交点为A,顶点为D、点P是该抛物线上的一个动点,过点P作
的抛物线经过B、C两点,与x轴的另一个交点为A,顶点为D、点P是该抛物线上的一个动点,过点P作![]() 轴于点E,分别交线段BD、BC于点F、G,设点P的横坐标为
轴于点E,分别交线段BD、BC于点F、G,设点P的横坐标为![]() .
.
![]() 求该抛物线所对应的函数关系式及顶点D的坐标;
求该抛物线所对应的函数关系式及顶点D的坐标;
![]() 求证:
求证:![]() ;
;![]() ;
;
![]() 当
当![]() 为等腰三角形时,求t的值.
为等腰三角形时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,![]() ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线EF//GH,且EF和GH之间的距离为1,小明同学制作了一个直角三角形硬纸板ACB,其中∠ACB=90°,∠BAC=60°,AC=1.小明利用这块三角板进行了如下的操作探究:
(1)如图1,若点C在直线EF上,且∠ACE=20°,求∠1的度数;
(2)若点A在直线EF上,点C在EF和GH之间(不含EF、GH上),边BC、AB与直线GH分别交于点D和点K.
①如图2,∠AKD、∠CDK的平分线交于点O.在△ABC绕着点A旋转的过程中,∠O的度数是否变化?若不变,求出∠O的度数:若变化,请说明理由;
②如图3,在△ABC绕着点A旋转的过程中,设∠EAK=n°,∠CDK=(4m-3n-10)°,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
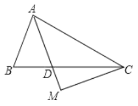
【题目】已知,如图,在△ABC 中,AD 平分∠BAC,AD=AB,CM⊥AD 于 M,请你通过观察和测量,猜想线段 AB、AC 之和与线段 AM 有怎样的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com