
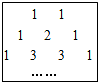
我国宋朝数学家杨辉在他的著作《详解九章算法》中提出右表,此表揭示了(a+b)n(n 为非负 数)展开式的各项系数的规律.例如:
(a+b)0=1,它只有一项,系数为 1;
(a+b)1=a+b,它有两项,系数分别为 1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为 1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为 1,3,3,1; 根据以上规律,(a+b)4 展开式共有五项,系数分别为 .
1,4,6,4,1 .
【考点】完全平方公式;规律型:数字的变化类.
【专题】压轴题;规律型.
【分析】由图可知,从第三行开始,除去首项和最后一项,其余项应该等于上一行与其列数相同的 数+上一行前一列的数.那么第五行的五个数就应该是 1,4,6,4,1.
【解答】解:(a+b)0=1,它只有一项,系数为 1;
(a+b)1=a+b,它有两项,系数分别为 1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为 1,2,1;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为 1,3,3,1; 所以(a+b)4 展开的五项系数应该为:1,4,6,4,1. 故答案为:1,4,6,4,1.
【点评】本题考查完全平方公式的推广,读懂题目信息,准确找出规律是解题的关键,这类题型在 2016 届中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化 的.


科目:初中数学 来源: 题型:
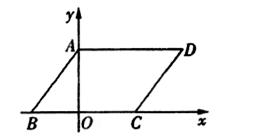
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方 程
程 的两个根,且OA>OB.
的两个根,且OA>OB.
(1)求OA、OB的长.
(2)若点E为x轴上的点,且S△AOE=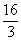 ,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似.
,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似.
 (3)若点M在平面直
(3)若点M在平面直 角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在▱ABCD 中,∠B﹣∠A=30°,则∠A,∠B,∠C,∠D 的度数是( )
A.95°,85°,95°,85° B.85°,95°,85°,95° C.105°,75°,105°,75° D.75°,105°,75°,105°
查看答案和解析>>
科目:初中数学 来源: 题型:
已知四个三角形分别满足下列条件:①三角形的三边之比为 1:1: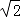 ;②三角形的三边分别 是 9、40、41;③三角形三内角之比为 1:2:3;④三角形一边上的中线等于这边的一半.其中直 角三角形有( )个.
;②三角形的三边分别 是 9、40、41;③三角形三内角之比为 1:2:3;④三角形一边上的中线等于这边的一半.其中直 角三角形有( )个.
A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com