
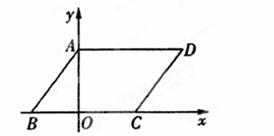
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方 程
程 的两个根,且OA>OB.
的两个根,且OA>OB.
(1)求OA、OB的长.
(2)若点E为x轴上的点,且S△AOE=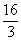 ,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似.
,求经过D、E两点的直线解析式,并判断△AOE与△AOD是否相似.
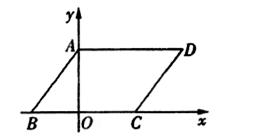 (3)若点M在平面直
(3)若点M在平面直 角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
(1)解一元二次方程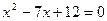
 |
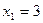 ,
,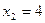
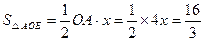
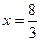
 ,0)或(
,0)或(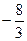 ,0), …………………3分
,0), …………………3分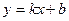
 ,0),(6,4)
,0),(6,4)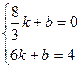 ,解得
,解得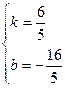
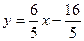 …………………4分
…………………4分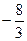 ,0),(6,4)
,0),(6,4)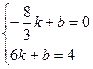 ,解得
,解得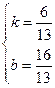
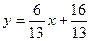 ………………… 5分
………………… 5分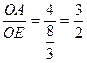 ,
,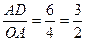
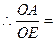
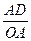
(3)符合条件的F点共有4个,其坐标分别为m
(- 3,0)或(3,8)或(
3,0)或(3,8)或(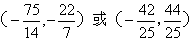 …………………10分
…………………10分


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
题面:下列命题说法中:
(1)等腰三角形一定是锐角三角形
(2)等腰三角形有一个外角等于120°,这 一个三角形一定是等边三角形
一个三角形一定是等边三角形
(3)等腰三角形中有一个外角为140°,那么它的底角为70°
(4)等腰三角形是轴对称图形,它有3条对称轴
错误的有( )个
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中,
①有一组邻边互相垂直的菱形是正方形
②若2x=3y,则
③若(﹣1,a)、(2,b)是双曲线y= 上的两点,则a>b
上的两点,则a>b
正确的有( )个
A.1 B.2 C.3 D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
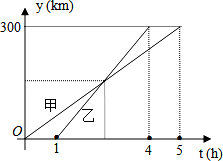
甲、乙两车从 A 城出发匀速行驶至 B 城.在整个行驶过程中,甲、乙两车离开 A 城的距离 y(千 米)与甲车行驶的时间 t(小时)之间的函数关系如图所示.则下列结论:
①A,B 两城相距 300 千米;
②乙车比甲车晚出发 1 小时,却早到 1 小时;
③乙车出发后 2.5 小时追上甲车;
④当甲、乙两车相距 50 千米时,t=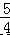 或
或  . 其中正确的结论有( )
. 其中正确的结论有( )
A.1 个 B.2 个 C.3 个 D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
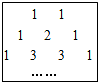
我国宋朝数学家杨辉在他的著作《详解九章算法》中提出右表,此表揭示了(a+b)n(n 为非负 数)展开式的各项系数的规律.例如:
(a+b)0=1,它只有一项,系数为 1;
(a+b)1=a+b,它有两项,系数分别为 1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为 1,2,1;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为 1,3,3,1; 根据以上规律,(a+b)4 展开式共有五项,系数分别为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com