
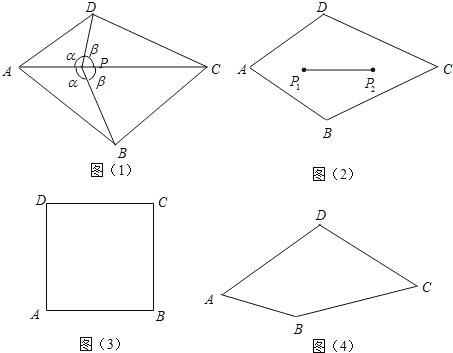
【题目】如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α.且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.
【1】在图(3)正方形ABCD内画一个半等角点P,且满足α≠β;
【2】在图(4)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法);
【3】若四边形ABCD有两个半等角点P1、P2(如图(2)),证明线段P1P2上任一点也是它的半等角点.
【答案】
【1】所画的点P在AC上且不是AC的中点和AC的端点.(2分)
【2】画点B关于AC的对称点B’,延长DB’交AC于点P,点P为所求(不写文字说明不扣分).(3分)
【3】连P1A、P1D、P1B、P1C和P2D、P2B,根据题意,
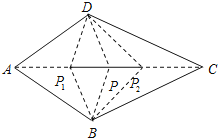
∠AP1D=∠AP1B,∠DP1C=∠BP1C,
∴∠AP1B+∠BP1C=180度.
∴P1在AC上,
同理,P2也在AC上.
在△DP1P2和△BP1P2中,
∠DP2P1=∠BP2P1,∠DP1P2=∠BP1P2,P1P2公共,
∴△DP1P2≌△BP1P2.
所以DP1=BP1,DP2=BP2,于是B、D关于AC对称.
设P是P1P2上任一点,连接PD、PB,由对称性,得∠DPA=∠BPA,∠DPC=∠BPC,
所以点P是四边形的半等角点.(5分)
【解析】(1)根据题意可知,所画的点P在AC上且不是AC的中点和AC的端点.因为在图形内部,所以不能是AC的端点,又由于α≠β,所以不是AC的中点.
(2)画点B关于AC的对称点B’,延长DB’交AC于点P,点P为所求.(因为对称的两个图形完全重合)
(3)先连P1A、P1D、P1B、P1C和P2D、P2B,根据题意∠AP1D=∠AP1B,∠DP1C=∠BP1C∴∠AP1B+∠BP1C=180度.∴P1在AC上,同理,P2也在AC上,再利用ASA证明△DP1P2≌△BP1P2而,那么△P1DP2和△P1BP2关于P1P2对称,P是对称轴上的点,所以∠DPA=∠BPA,∠DPC=∠BPC.即点P是四边形的半等角点


科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() .
.
(1) 若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2) 如图,反比例函数![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移至C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移至C2处所扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】肥皂泡的泡壁厚度大约是0.0007mm,0.0007用科学记数法表示为( )
A.0.7×10﹣3
B.7×10﹣3
C.7×10﹣4
D.7×10﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着十一黄金周的来临,父亲、儿子、女儿三人准备外出旅游,咨询了解到甲旅行社的规定:大人买一张全票,两个孩子的费用可按全票价的一半优惠;乙旅行社规定:三人可按团体票价计价,即按原价的60%收费.已知两个旅行社的原票价相同,问选择哪个旅行社省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苹果每千克m元,买10千克以上8.5折优惠(即按原价的85%出售),买30千克应付( )
A. 30×(1+85%)m元 B. 30×(1﹣85%)m元 C. 30×85%m元 D. 30m元
查看答案和解析>>
科目:初中数学 来源: 题型:
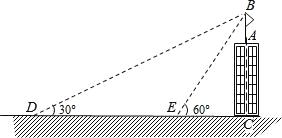
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:≈1.73,≈1.41.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com