
【题目】从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解”雾霾天气的主要原因“,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完整的统计图表.
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题: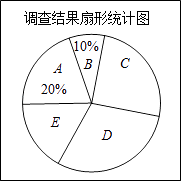
(1)填空:m= , n= . 扇形统计图中E组所占的百分比为%;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
【答案】
(1)40;100;15
(2)解:100× ![]() =30(万人);
=30(万人);
所以持D组“观点”的市民人数为30万人
(3)解:随机抽查一人,则此人持C组“观点”的概率是 ![]() =
= ![]() .
.
答:随机抽查一人,则此人持C组“观点”的概率是 ![]()
【解析】解:(1)总人数是:80÷20%=400(人),则m=400×10%=40(人), C组的频数n=400﹣80﹣40﹣120﹣60=100(人),
E组所占的百分比是: ![]() ×100%=15%;
×100%=15%;
所以答案是:40,100,15%;
【考点精析】解答此题的关键在于理解扇形统计图的相关知识,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况,以及对概率公式的理解,了解一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】采摘茶叶是茶农一项很繁重的劳动,利用单人便携式采茶机能大大提高生产效率.实践证明,一台采茶机每天可采茶60公斤,是人手工采摘的5倍,购买一台采茶机需2400元.茶园雇人采摘茶叶,按每采摘1公斤茶叶m元的标准支付雇工工资,一个雇工手工采摘茶叶20天获得的全部工钱正好购买一台采茶机.
(1)求m的值;
(2)有两家茶叶种植户王家和顾家均雇人采摘茶叶,王家雇用的人数是顾家的2倍.王家所雇的人中有![]() 的人自带采茶机采摘,
的人自带采茶机采摘, ![]() 的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=____________;
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y | … | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | … |
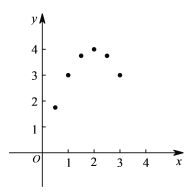
写出m=____________;
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得,x=____________时,矩形的面积最大;写出该函数的其它性质(一条即可):____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 . 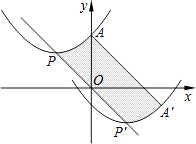
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s). 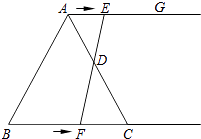
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空: ①当t为s时,四边形ACFE是菱形;
②当t为s时,以A、F、C、E为顶点的四边形是直角梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
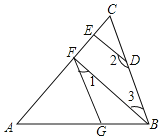
【题目】如图,![]() 于点E,
于点E,![]() 于点F,
于点F,![]() ,求证:
,求证:![]() .
.
试将下面的证明过程补充完整![]() 填空
填空![]() :
:
证明:![]() ,
,![]() 已知
已知![]()
![]() ______
______![]()
![]() 同位角相等,两直线平行
同位角相等,两直线平行![]() ,
,
![]() 两直线平行,同旁内角互补
两直线平行,同旁内角互补![]() ,
,
又![]() 已知
已知![]() ,
,
![]() ______,
______,![]() 同角的补角相等
同角的补角相等![]()
![]() ______
______![]() 内错角相等,两直线平行
内错角相等,两直线平行![]() ,
,
![]() ______
______![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
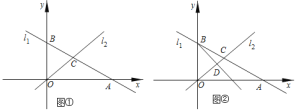
【题目】在平面直角坐标系中,直线![]() :
:![]() 分别与x轴、y轴交于点A、点B,且与直线
分别与x轴、y轴交于点A、点B,且与直线![]() :
:![]() 于点C.
于点C.
![]() Ⅰ
Ⅰ![]() 如图
如图![]() ,求出B、C两点的坐标;
,求出B、C两点的坐标;
![]() Ⅱ
Ⅱ![]() 若D是线段OC上的点,且
若D是线段OC上的点,且![]() 的面积为4,求直线BD的函数解析式.
的面积为4,求直线BD的函数解析式.
![]() Ⅲ
Ⅲ![]() 如图
如图![]() ,在
,在![]() Ⅱ
Ⅱ![]() 的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com