
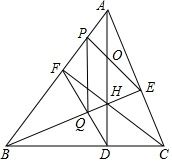
 如图,AD、BE、CF是锐角△ABC的三条高,H为垂心,取AH的中点O,射线EO交AB于点P,DF交BE于点Q,求证:PQ⊥BC.
如图,AD、BE、CF是锐角△ABC的三条高,H为垂心,取AH的中点O,射线EO交AB于点P,DF交BE于点Q,求证:PQ⊥BC. 分析 根据高线的性质,可得∠AFC=∠ADC=90°,根据垂心性质,可得四点共圆,根据余角的性质,可得∠PEH+∠HFQ=90°,再根据四点共圆的判定与性质,可得∠PQE=∠PFE,∠PQE=∠AHE,根据平行线的判定,可得PQ∥AH.
解答 证明:如图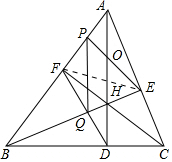 ,
,
∵AD、BE、CF是锐角△ABC的三条高,
∴∠BFD+∠CFD=90°,∠AEO+∠PEH=90°.
∵∠AFC=∠ADC=90°,
∴A、F、D、C四点共圆,
∴∠DFC=∠DAC.
∵OE是Rt△斜边上的中线,
∴AO=OE,
∴∠OAE=∠OEA.
∴∠PEH+∠HFQ=90°,
∴∠PEQ+∠PFQ=180°.
∴FQEP四点共圆.
∴∠PQE=∠PFE.
∵A、F、H、E四点共圆,
∴∠AFE=∠AHE,
∴∠PQE=∠AHE,
∴PQ∥AH
∴PQ⊥BC.
点评 本题考查了三角形的五心,利用垂心的性质得出四点共圆是解题关键,又利用同弦所对的圆周角相等.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:选择题
 如图所示,数轴上两点A、B分别表示两个有理数a、b,则下列四个数中最小的一个数是( )
如图所示,数轴上两点A、B分别表示两个有理数a、b,则下列四个数中最小的一个数是( )| A. | -$\frac{1}{b}$ | B. | $\frac{1}{a}$ | C. | a | D. | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100° | B. | 100°或20° | C. | 50° | D. | 50°或10° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
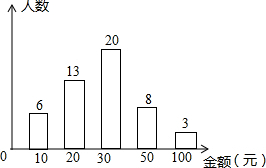 抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )| A. | 20,20 | B. | 30,20 | C. | 30,30 | D. | 20,30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com