
(本小题满分10分)已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为点E,点F在BD上,连接AF,EF.

(1)求证:AD=ED;
(2)如果AF∥CD,求证:四边形ADEF是菱形.
见解析
【解析】
试题分析:(1)根据条件证明ΔABD≌ΔEBD,可得AD=ED;(2)由(1)知AD=ED,所以要证明四边形ADEF是菱形,只需要证明AF∥DE,AF=DE,得四边形ADEF是平行四边形即可.
试题解析:证明:(1)∵BC=CD,∴∠CDB=∠CBD.
∵AD∥BC,∴∠ADB=∠CBD.∴∠ADB=∠CDB.(2分)
又∵AB⊥AD,BE⊥CD,∴∠BAD=∠BED=90°.
于是,在ΔABD和ΔEBD中,∵∠ADB=∠CDB,
∠BAD=∠BED,BD=BD,∴ΔABD≌ΔEBD. (4分)
∴AD=ED. (5分)
(2) ∵AF∥CD,∴∠AFD=∠EDF.
∴∠AFD=∠ADF,即得AF=AD. (7分)
又∵AD=ED,∴AF=DE.
于是,由AF∥DE,AF=DE,
得四边形ADEF是平行四边形. (9分)
又∵AD=ED,∴四边形ADEF是菱形. (10分)
考点:1. 等腰三角形的性质2. 全等三角形的判定与性质;3. 菱形的判定.


科目:初中数学 来源:2014-2015学年山东省新泰市九年级上学期学业水平模拟数学试卷(解析版) 题型:选择题
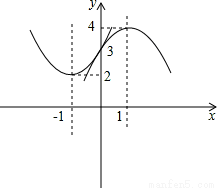
在平面直角坐标系中,将抛物线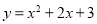 绕着它与
绕着它与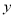 轴的交点旋转180°,所得抛物线的解析式是( ).
轴的交点旋转180°,所得抛物线的解析式是( ).
A.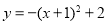 B.
B.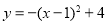
C. D.
D.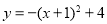
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级下学期学业水平模拟考试1数学试卷(解析版) 题型:解答题
(本小题满分12分)我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A,B重合),D是半圆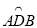 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.

①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
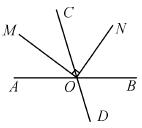
如图,直线AB、CD相交于O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:解答题
(本小题满分10分)
方法介绍:
同学们,生活中的很多实际问题,我们往往抽象成数学问题,然后通过数形结合建立数学模型的方式来解决.
例如:学校举办足球赛,共有五个球队参加比赛,每个队都要和其他各队比赛一场,问该学校一共要安排多少场比赛?
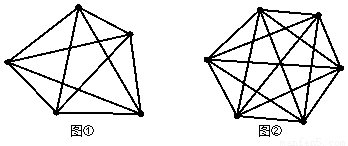
这是一个实际问题,我们可以在平面内画出5个点(任意3个点都不在同一条直线上),如图①所示,其中每个点各代表一个足球队,两个队之间比赛一场就用一条线段把他们连起来,其中连接线段的条数就是安排比赛的场数.这样模型就建立起来了,如何解决这个模型呢?由于每个队都要与其他各队比赛一场,即每个点都要与另外4点连接一条线段,这样5个点应该有5×4=20条线段,而每两个点之间的线段都重复计算了一次,实际只有10条线段,所以学校一共要安排10场比赛.
学以致用:
(1)根据图②回答:如果有6个班级的足球队参加比赛,学校一共要安排 场比赛;
(2)根据规律,如果有n个班级的足球队参加比赛,学校一共要安排 场比赛.
问题解决:
(1)小明今年参加了学校新组建的合唱队,老师让所有人每两人相互握手,认识彼此(每两人之间不重复握手).小明发现所有人握手次数总和为91次,那么合唱队有多少人?
(2)A、B、C、D、E、F六人参加一次会议,见面时他们相互握手问好,每两人之间不重复握手,如图③,已知A已经握了5次,B已经握了4次,C已经握了3次,D已经握了2次,E已经握了1次,请利用图③分析F已经和哪些人握手了.

问题拓展:
根据上述模型的建立和问题的解决,请你提出一个问题,并进行解答.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:填空题
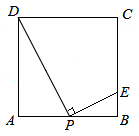
如图,在边长10cm为的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为 cm。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com