
【题目】某公司经销一种成本为10元的产品,经市场调查发现,在一段时间内,销售量![]() (件)与销售单价
(件)与销售单价![]() ( 元/件 )的关系如下表:
( 元/件 )的关系如下表:
|
| 15 | 20 | 25 | 30 |
|
|
| 550 | 500 | 450 | 400 |
|
设这种产品在这段时间内的销售利润为![]() (元),解答下列问题:
(元),解答下列问题:
(1)如![]() 是
是![]() 的一次函数,求
的一次函数,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求销售利润![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(3)求当![]() 为何值时,
为何值时,![]() 的值最大?最大是多少?
的值最大?最大是多少?
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.25人中至少有3人的出生月份相同
B.任意抛掷一枚均匀的1元硬币,若上一次正面朝上,则下一次一定反面朝上
C.天气预报说明天降雨的概率为10%,则明天一定是晴天
D.任意抛掷一枚均匀的骰子,掷出的点数小于3的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是小区常见的漫步机,从侧面看如图2,踏板静止时,踏板连杆与立柱![]() 上的线段
上的线段![]() 重合,
重合,![]() 长为0.2米,当踏板连杆绕着点
长为0.2米,当踏板连杆绕着点![]() 旋转到
旋转到![]() 处时,测得
处时,测得![]() ,此时点
,此时点![]() 距离地面的高度
距离地面的高度![]() 为0.44米.求:
为0.44米.求:

(1)踏板连杆![]() 的长.
的长.
(2)此时点![]() 到立柱
到立柱![]() 的距离.(参考数据:
的距离.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()
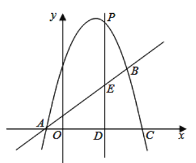
(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
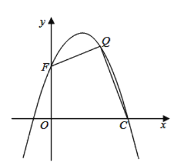
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 箱中装有3张相同的卡片,它们分别写有数字1,2,4;
箱中装有3张相同的卡片,它们分别写有数字1,2,4;![]() 箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从
箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从![]() 箱、
箱、![]() 箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率.
(2)如果取出![]() 箱中卡片上的数字作为十位上的数字,取出
箱中卡片上的数字作为十位上的数字,取出![]() 箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中如图:
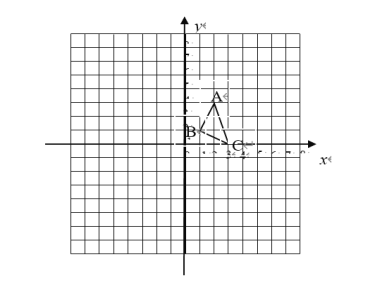
(1)画出将△ABC绕点O逆时针旋转90°所得到的![]() ,并写出
,并写出![]() 点的坐标.
点的坐标.
(2)画出将△ABC关于x轴对称的![]() ,并写出
,并写出![]() 点的坐标.
点的坐标.
(3)求在旋转过程中线段OA扫过的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
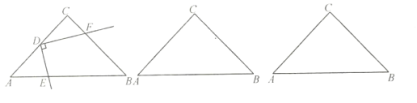
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
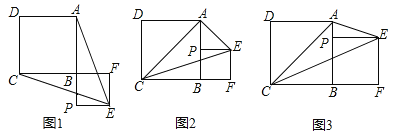
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为边
为边![]() 上一动点,点
上一动点,点![]() 为射线
为射线![]() 上一动点,且
上一动点,且![]() .
.
(1)当![]() 时,联结
时,联结![]() ,求
,求![]() 的余切值;
的余切值;
(2)当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)联结![]() ,若
,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
(1)求反比例函数的表达式:
(2)画出直线和双曲线的示意图;
(3)直接写出![]() 的解集______;
的解集______;
(4)若点![]() 是坐标轴负半轴上一点,且满足
是坐标轴负半轴上一点,且满足![]() .直接写出点
.直接写出点![]() 的坐标______.
的坐标______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com