
【题目】甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离![]() 与运动时间
与运动时间![]() 的函数关系大致如图所示,下列说法中错误的是( ).
的函数关系大致如图所示,下列说法中错误的是( ).
A.两人出发1小时后相遇B.赵明阳跑步的速度为![]()
C.王浩月到达目的地时两人相距![]() D.王浩月比赵明阳提前
D.王浩月比赵明阳提前![]() 到目的地
到目的地
【答案】C
【解析】
根据图像可得两地之间的距离,再分别算出两人的行进速度,据此可得各项数据进而判断各选项.
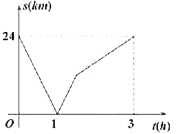
解:由图可知:当时间为0h时,两人相距24km,
即甲乙两地相距24km,
当时间为1h时,甲乙两人之间距离为0,
即此时两人相遇,故A正确;
∵24÷1=24,可得两人的速度和为24km/h,
由于王浩月先到达目的地,故赵明阳全程用了3h,
∴赵明阳的速度为24÷3=8km/h,故B正确;
可知王浩月的速度为24-8=16km/h,
∴王浩月到达目的地时,用了24÷16=![]() h,
h,
此时赵明阳行进的路程为:![]() ×8=12km,
×8=12km,
即此时两人相距12km,故C错误;
赵明阳到达目的地时,用了3h,
则3-![]() =
=![]() =1.5h,
=1.5h,
∴王浩月比赵明阳提前1.5h到目的地,故D正确.
故选C.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.点C在
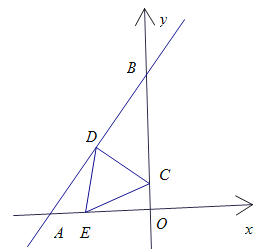
轴相交于点B.点C在![]() 轴上运动,作CD⊥AB,垂足为D.点E为
轴上运动,作CD⊥AB,垂足为D.点E为![]() 轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
(1)用n表示线段CD的长;
(2)当OC=1时,若点F落在直线y轴上,求此时点E的坐标;
(3)在点E的运动过程中,若存在唯一的位置,使得四边形CEDF为矩形,请直接写出点C的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CBA球赛已经开始,某体育用品商店预测某球队的球服能够畅销,就用![]() 万元购入了一批球服,上市后很快就脱销,该商店又用
万元购入了一批球服,上市后很快就脱销,该商店又用![]() 万元购入第二批该球队的球服,所购数量是第一批购入数量的2倍,但每套进价多了10 元.如果该商店购入的两批球服售价一样,且要求两批球服全部售完后总利润率不低于
万元购入第二批该球队的球服,所购数量是第一批购入数量的2倍,但每套进价多了10 元.如果该商店购入的两批球服售价一样,且要求两批球服全部售完后总利润率不低于![]() ,那么每套球服的售价至少是( )元.(利润率
,那么每套球服的售价至少是( )元.(利润率![]() 利润
利润![]() 成本
成本![]() )
)
A.160B.180C.200D.220
查看答案和解析>>
科目:初中数学 来源: 题型:
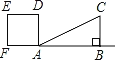
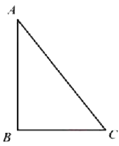
【题目】如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )
A.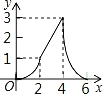 B.
B.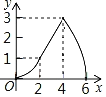
C.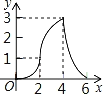 D.
D.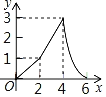
查看答案和解析>>
科目:初中数学 来源: 题型:
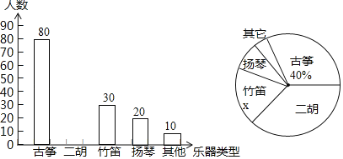
【题目】某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集到的数据绘制成如下两幅不完整的统计图.
(1)这次共抽取 学生调查,扇形统计图中的x= ;
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是多少度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
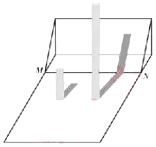
【题目】实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线![]() 的距离皆为
的距离皆为![]() .王诗嬑观测到高度
.王诗嬑观测到高度![]() 矮圆柱的影子落在地面上,其长为
矮圆柱的影子落在地面上,其长为![]() ;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线
;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线![]() 互相垂直,并视太阳光为平行光,测得斜坡坡度
互相垂直,并视太阳光为平行光,测得斜坡坡度![]() ,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:
,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:
(1)若王诗嬑的身高为![]() ,且此刻她的影子完全落在地面上,则影子长为多少
,且此刻她的影子完全落在地面上,则影子长为多少![]() ?
?
(2)猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否正确?
(3)若同一时间量得高圆柱落在坡面上的影子长为![]() ,则高圆柱的高度为多少
,则高圆柱的高度为多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x+1与y轴交于点A,与双曲线![]() (x>0)交于点B(2,a).
(x>0)交于点B(2,a).
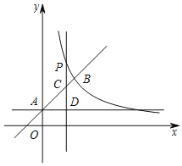
(1)求a,k的值.
(2)点P是直线l上方的双曲线上一点,过点P作平行于y轴的直线,交直线l于点C,过点A作平行于x轴的直线,交直线PC于点D,设点P的横坐标为m.
①若m=![]() ,试判断线段CP与CD的数量关系,并说明理由;②若CP>CD,请结合函数图象,直接写出m的取值范围.
,试判断线段CP与CD的数量关系,并说明理由;②若CP>CD,请结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划一次性购进甲、乙两种商品共![]() 件,甲、乙两种商品的进价和售价如下表所示:
件,甲、乙两种商品的进价和售价如下表所示:
甲 | 乙 | |
进价(元/件) | 100 | 80 |
售价(元/件) | 150 | 120 |
设购进甲种商品的数量为![]() 件.
件.
(1)设进货成本为![]() 元,求
元,求![]() 与
与![]() 之间的函数解析式;若购进甲种商品的数量不少于
之间的函数解析式;若购进甲种商品的数量不少于![]() 件,则最低进货成本是多少元?
件,则最低进货成本是多少元?
(2)若除了进货成本,还要支付运费和销售员工工资共![]() 元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价
元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价![]() 元
元![]() ,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为
,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为![]() 元.
元.
①每件甲种商品的利润是 元(用含![]() 的代数式表示)
的代数式表示)
②求![]() 关于
关于![]() 的函数解析式
的函数解析式
③当![]() 时,请你根据
时,请你根据![]() 的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
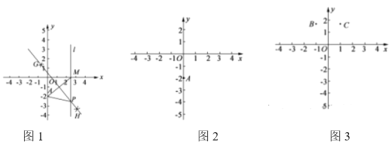
【题目】如图1,在平面直角坐标系中,点A的坐标是![]() ,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于
,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于![]() 的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为________,其理由为:________________.
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
M的坐标 | … |
|
|
|
| … |
P的坐标 | … |
|
| … |
猜想:
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线L,猜想曲线L的形状是________.
验证:
(4)设点P的坐标是![]() ,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
(5)如图3,点![]() ,
,![]() ,求点D的纵坐标
,求点D的纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com