
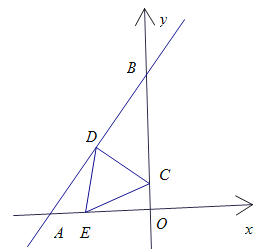
【题目】已知直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.点C在
轴相交于点B.点C在![]() 轴上运动,作CD⊥AB,垂足为D.点E为
轴上运动,作CD⊥AB,垂足为D.点E为![]() 轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
(1)用n表示线段CD的长;
(2)当OC=1时,若点F落在直线y轴上,求此时点E的坐标;
(3)在点E的运动过程中,若存在唯一的位置,使得四边形CEDF为矩形,请直接写出点C的坐标
【答案】(1)![]() ;(2)
;(2)![]() ;(3)C的坐标为(0,0)或(0,
;(3)C的坐标为(0,0)或(0,![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() )
)
【解析】
(1)先求出A,B坐标,然后表示出BC,OA,BA,再证明△BCD∽△BAO,得出![]() ,即可求出CD;
,即可求出CD;
(2)先求出CD的解析式,然后联立CD和AB的解析式得出D的坐标为,设CD的中点为G,得出G的坐标为(![]() ),然后根EF关于G对称,且F在y轴,可求出答案;
),然后根EF关于G对称,且F在y轴,可求出答案;
(3)根据题意得要想让四边形CEDF为矩形,则有C,E,D,F四点共圆,可推出四种情况①点C与点O重合;②点C在线段OB上;③点D与点A重合;④点C在y负半轴上,且以CD为直径的圆与x轴相切,分别讨论即可.
解:(1)由题意可求出直线![]() 与
与![]() 轴相交于点A的坐标为(-3,0),与
轴相交于点A的坐标为(-3,0),与![]() 轴相交于点B的坐标为(0,4),
轴相交于点B的坐标为(0,4),
∵点C的坐标为(0,n),
∴BC=4-n,OA=3,BA=5,
∵CD⊥AB,∠DBC=∠ABO,
∴△BCD∽△BAO,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵OC=1,
∴C(0,1),
∵CD⊥AB,
∴kCD·kAB=-1,
∵kAB=![]() ,
,
∴kCD=![]() ,
,
∴设CD的解析式为y=![]() x+b,
x+b,
将C代入得b=1,
∴CD的解析式为y=![]() x+1,
x+1,
联立CD和AB的解析式得: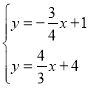 ,
,
解得: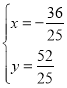 ,
,
∴D的坐标为(![]() ),
),
设CD的中点为G,
∴G的坐标为(![]() ),
),
∵EF关于G对称,且F在y轴,
∴xG-xE=0-xG,
xE=![]() ,
,
∴![]() ;
;
(3)要想让四边形CEDF为矩形,
根据矩形的性质可知这四点共圆,圆心为CD中点G,
如图,可得出四种情况,
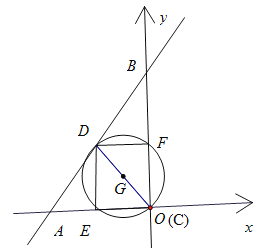
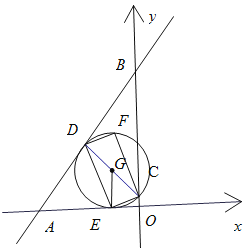
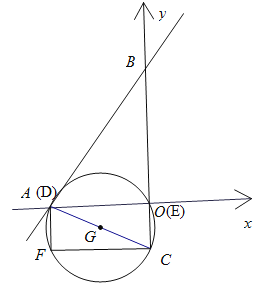
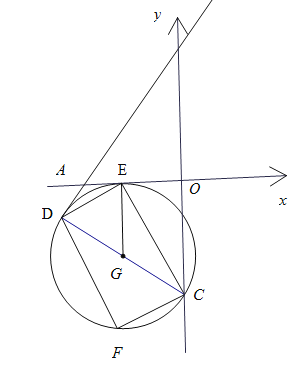
①点C与点O重合,此时C的坐标为(0,0);
②点C在线段OB上,此时以CD为直径的圆与x轴相切,
设CD的解析式为:y=![]() x+n,
x+n,
联立CD和AB的解析式可得D的坐标为(![]() ),
),
∴点G的坐标为(![]() ),
),
∵以CD为直径的圆与x轴相切,
∴GE⊥x轴,
∴点E的横坐标与点G相同,
∴E的坐标为(![]() ,0),
,0),
∵![]() CD=GE,
CD=GE,
∴可得![]() ×
×![]() =
=![]() ,
,
解得n=![]() ,
,
∴C的坐标为(0,![]() );
);
③点D与点A重合,
此时D的坐标为(-4,0),E的坐标为(0,0),
∵四边形
∴根据勾股定理可得![]() =
=![]() ,
,
解得n=![]()
∴C的坐标为:(0,![]() );
);
④点C在y负半轴上,且以CD为直径的圆与x轴相切,
由②可得此时![]() ×
×![]() =-
=-![]() ,
,
解得n=![]() ,
,
∴C的坐标为:(0,![]() );
);
综上,C的坐标为:(0,0)或(0,![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于
交x轴于![]() ,
,![]() 两点,与y轴交于点C,AC,BC.M为线段OB上的一个动点,过点M作
两点,与y轴交于点C,AC,BC.M为线段OB上的一个动点,过点M作![]() 轴,交抛物线于点P,交BC于点Q.
轴,交抛物线于点P,交BC于点Q.
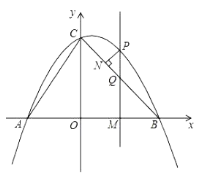
(1)求抛物线的表达式;
(2)过点P作![]() ,垂足为点N.设M点的坐标为
,垂足为点N.设M点的坐标为![]() ,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?
,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?
(3)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
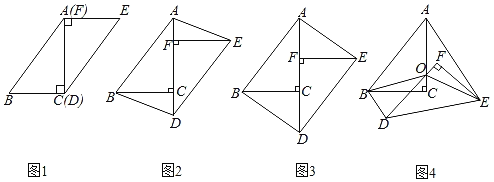
【题目】在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(思考)图2中的四边形ABDE是平行四边形吗?请说明理由.
(发现)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.
活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
(探究)当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用40天社会实践参与了某加盟店经营,他销售了一种成本为20元/件的商品,细心的他发现在第![]() 天销售的相关数据可近似地用如下表中的函数表示:
天销售的相关数据可近似地用如下表中的函数表示:
销售量 | 销售单价 | |
| 当 | 当 |
(1)求前20天第几天获得的利润最大?最大利润是多少?
(2)求后20天第几天获得的利润最大?最大利润是多少?
(3)在后20天中,他决定每销售一件商品给山区孩子捐款![]() 元(
元(![]() 且
且![]() 为整数),此时若还要求每一天的利润都不低于160元,求
为整数),此时若还要求每一天的利润都不低于160元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
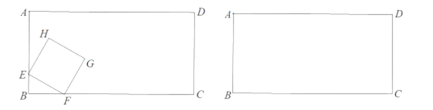
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
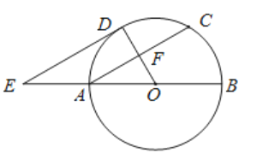
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为弦
为弦![]() 的中点,连接
的中点,连接![]() 并延长交弧
并延长交弧![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() 、
、![]() 、
、![]() .填空
.填空
①当![]() 的度数为_______时,四边形
的度数为_______时,四边形![]() 为菱形;
为菱形;
②当![]() 时,四边形
时,四边形![]() 的面积为_______.
的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海市有A,B,C,D,E五个景区很受游客喜爱.对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图.
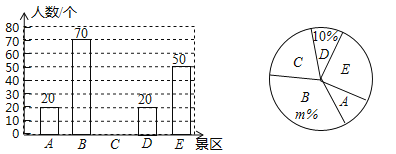
(1)该小区居民在这次随机调查中被调查到的人数是 人,m= ;
(2)若该小区有居民1500人,试估计去C景区旅游的居民约有多少人?
(3)甲、乙两人暑假打算游玩,甲从B、C两个景点中任意选择一个游玩,乙从B、C 、E三个景点中任意选择一个游玩.求甲、乙恰好游玩同一景点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 同时出发,点
同时出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿边
个单位长度的速度沿边![]() 向终点匀速运动,点
向终点匀速运动,点![]() 以每秒
以每秒![]() 个单位长度的速度沿边
个单位长度的速度沿边![]() 向终点匀速运动,以
向终点匀速运动,以![]() 为边在边
为边在边![]() 上方作正方形
上方作正方形![]() 设点
设点![]() 运动时间为
运动时间为![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)当点![]() 落在边
落在边![]() 上时,求此时
上时,求此时![]() 的值;
的值;
(3)设正方形![]() 与矩形
与矩形![]() 重叠图形的面积为
重叠图形的面积为![]() 请直接写出
请直接写出![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离![]() 与运动时间
与运动时间![]() 的函数关系大致如图所示,下列说法中错误的是( ).
的函数关系大致如图所示,下列说法中错误的是( ).
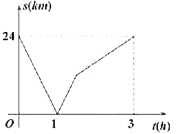
A.两人出发1小时后相遇B.赵明阳跑步的速度为![]()
C.王浩月到达目的地时两人相距![]() D.王浩月比赵明阳提前
D.王浩月比赵明阳提前![]() 到目的地
到目的地
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com