
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为弦
为弦![]() 的中点,连接
的中点,连接![]() 并延长交弧
并延长交弧![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
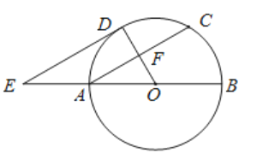
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() 、
、![]() 、
、![]() .填空
.填空
①当![]() 的度数为_______时,四边形
的度数为_______时,四边形![]() 为菱形;
为菱形;
②当![]() 时,四边形
时,四边形![]() 的面积为_______.
的面积为_______.
【答案】(1)证明见解析(2)①![]() ;②
;②![]()
【解析】
(1)根据![]() 为弦
为弦![]() 的中点证得FO⊥AC,再利用
的中点证得FO⊥AC,再利用![]() 得到OD⊥DE即可得到结论;
得到OD⊥DE即可得到结论;
(2)①连接![]() 、
、![]() 、
、![]() ,证明△AOD是等边三角形,得到DF=FO,证得四边形AOCD是平行四边形,再由AO=CO,即可得到四边形
,证明△AOD是等边三角形,得到DF=FO,证得四边形AOCD是平行四边形,再由AO=CO,即可得到四边形![]() 为菱形;
为菱形;
②连接CD,证明△AFO∽△ODE,得到![]() ,求出OD=2OF,DE=2AF,可证四边形ACDE是平行四边形,由勾股定理求出
,求出OD=2OF,DE=2AF,可证四边形ACDE是平行四边形,由勾股定理求出![]() ,即可求出四边形ACDE的面积.
,即可求出四边形ACDE的面积.
证明:(1)![]() 为弦
为弦![]() 的中点,
的中点,
![]() ,且
,且![]() 过圆心
过圆心![]() .
.
![]() ,
,
又![]() ,
,
![]() .
.
![]() 是
是![]() 切线
切线
(2)①当![]() =
=![]() 时,四边形AOCD是菱形,理由如下:
时,四边形AOCD是菱形,理由如下:
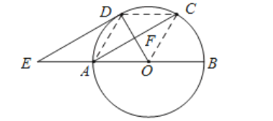
如图,连接![]() 、
、![]() 、
、![]() ,
,
∵![]() =
=![]() ,OF⊥AC,
,OF⊥AC,
∴∠AOF=60°,
∵AO=DO,
∴△AOD是等边三角形,
∵AF⊥DO,
∴DF=FO,
∵AF=FC,
∴四边形AOCD是平行四边形,
∵AO=CO,
故答案为:![]() ;
;
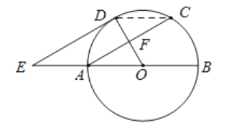
②连接CD,
∵AC∥DE,
∴△AFO∽△ODE,
∴![]() ,
,
∴OD=2OF,DE=2AF,
∵AC=2AF,
∴DE=AC,且DE∥AC,
∴四边形ACDE是平行四边形,
∵OA=AE=OD=2,
∴OF=DF=1,OE=4,
∵在Rt△ODE中,![]() ,
,
∴四边形ACDE的面积=![]() ,
,
故答案为:![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】山地自行车越来越受年轻人的喜爱.某车行经营的A型山地自行车去年销售总额为30万元,今年每辆车售价比去年降低了200元.若卖出的数量相同,销售总额将比去年减少10%,
(1)今年A型车每辆售价多少元?
(2)该车行计划再进一批A型车和新款B型车共60辆,要使这批车获利不少于4万元,A型车至多进多少辆?
A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元) | 1200 | 1400 |
销售价格(元) | 今年的销售价格 | 2200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生一分钟跳绳情况,从这两个年级随机抽取![]() 名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
七年级学生一分钟跳绳成绩频数分布直方图
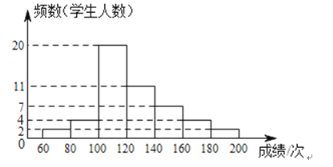
七、八年级学生一分钟跳绳成绩分析表

七年级学生一分钟跳绳成绩(数据分![]() 组:
组:![]() )在
)在![]() 这一组的是:
这一组的是:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
根据以上信息,回答下列问题:
![]() 表中
表中![]() ;
;
![]() 在这次测试中,七年级甲同学的成绩
在这次测试中,七年级甲同学的成绩![]() 次,八年级乙同学的成绩
次,八年级乙同学的成绩![]() ,他们的测试成绩,在各自年级所抽取的
,他们的测试成绩,在各自年级所抽取的![]() 名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
![]() 该校七年级共有
该校七年级共有![]() 名学生,估计一分钟跳绳不低于
名学生,估计一分钟跳绳不低于![]() 次的有多少人?
次的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018无锡市体育中考男生项目分为速度耐力类、力量类和灵巧类,每位考生只能在三类中各选一项进行考试.其中速度耐力类项目有:50米跑、800米跑、50米游泳;力量类项目有:掷实心球、引体向上;灵巧类项目有:30秒钟跳绳、立定跳远、俯卧撑、篮球运球.男生小明“50米跑”是强项,他决定必选,其它项目在平时测试中成绩完全相同,他决定随机选择.
(1)请用画树状图或列表的方法求“小明‘选50米跑、引体向上和立定跳远’”的概率;
(2)小明所选的项目中有立定跳远的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
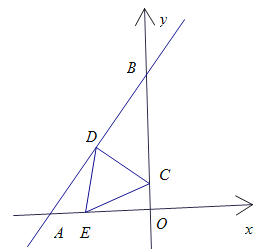
【题目】已知直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.点C在
轴相交于点B.点C在![]() 轴上运动,作CD⊥AB,垂足为D.点E为
轴上运动,作CD⊥AB,垂足为D.点E为![]() 轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
(1)用n表示线段CD的长;
(2)当OC=1时,若点F落在直线y轴上,求此时点E的坐标;
(3)在点E的运动过程中,若存在唯一的位置,使得四边形CEDF为矩形,请直接写出点C的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中
①三角形的外心到三角形的三个顶点的距离相等
②两条对角线相等的四边形是矩形
③将一次函数y=3x﹣1的图象不经过第四象限
④点A(x1,y1),B(x2,y2)都在反比例函数y=![]() 图象上,且x1<x2,则y1<y2
图象上,且x1<x2,则y1<y2
其中真命题有( )个
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
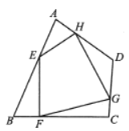
【题目】如图,在任意四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 上的点,对于四边形
上的点,对于四边形![]() 的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
A.当![]() ,
,![]() ,
,![]() ,
,![]() 是各边中点,且
是各边中点,且![]() 时,四边形
时,四边形![]() 为菱形
为菱形
B.当![]() ,
,![]() ,
,![]() ,
,![]() 是各边中点,且
是各边中点,且![]() 时,四边形
时,四边形![]() 为矩形
为矩形
C.当![]() ,
,![]() ,
,![]() ,
,![]() 不是各边中点时,四边形
不是各边中点时,四边形![]() 可以为平行四边形
可以为平行四边形
D.当![]() ,
,![]() ,
,![]() ,
,![]() 不是各边中点时,四边形
不是各边中点时,四边形![]() 不可能为菱形
不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
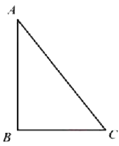
【题目】在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.

(1)作出△ABC关于y轴对称的△A1B1C1,其中点A,B,C分别和点A1,B1,C1对应;
(2)平移△ABC,使得点A在x轴上,点B在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中点A,B,C分别和点A2,B2,C2对应;
(3)直接写出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
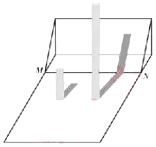
【题目】实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线![]() 的距离皆为
的距离皆为![]() .王诗嬑观测到高度
.王诗嬑观测到高度![]() 矮圆柱的影子落在地面上,其长为
矮圆柱的影子落在地面上,其长为![]() ;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线
;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线![]() 互相垂直,并视太阳光为平行光,测得斜坡坡度
互相垂直,并视太阳光为平行光,测得斜坡坡度![]() ,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:
,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:
(1)若王诗嬑的身高为![]() ,且此刻她的影子完全落在地面上,则影子长为多少
,且此刻她的影子完全落在地面上,则影子长为多少![]() ?
?
(2)猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否正确?
(3)若同一时间量得高圆柱落在坡面上的影子长为![]() ,则高圆柱的高度为多少
,则高圆柱的高度为多少![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com