
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЪЧ![]() ЃЌдкxжсЩЯШЮШЁвЛЕуMЃЎСЌНгAMЃЌЗжБ№вдЕуAКЭЕуMЮЊдВаФЃЌДѓгк
ЃЌдкxжсЩЯШЮШЁвЛЕуMЃЎСЌНгAMЃЌЗжБ№вдЕуAКЭЕуMЮЊдВаФЃЌДѓгк![]() ЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгкGЃЌHСНЕуЃЌзїжБЯпGHЃЌЙ§ЕуMзїxжсЕФДЙЯпlНЛжБЯпGHгкЕуPЃЎИљОнвдЩЯВйзїЃЌЭъГЩЯТСаЮЪЬтЃЎ
ЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгкGЃЌHСНЕуЃЌзїжБЯпGHЃЌЙ§ЕуMзїxжсЕФДЙЯпlНЛжБЯпGHгкЕуPЃЎИљОнвдЩЯВйзїЃЌЭъГЩЯТСаЮЪЬтЃЎ
ЬНОПЃК
ЃЈ1ЃЉЯпЖЮPAгыPMЕФЪ§СПЙиЯЕЮЊ________ЃЌЦфРэгЩЮЊЃК________________ЃЎ
ЃЈ2ЃЉдкxжсЩЯЖрДЮИФБфЕуMЕФЮЛжУЃЌАДЩЯЪізїЭМЗНЗЈЕУЕНЯргІЕуPЕФзјБъЃЌВЂЭъГЩЯТСаБэИёЃК
MЕФзјБъ | Ё |
|
|
|
| Ё |
PЕФзјБъ | Ё |
|
| Ё |
ВТЯыЃК
ЃЈ3ЃЉЧыИљОнЩЯЪіБэИёжаPЕуЕФзјБъЃЌАбетаЉЕугУЦНЛЌЕФЧњЯпдкЭМ2жаСЌНгЦ№РДЃЛЙлВьЛГіЕФЧњЯпLЃЌВТЯыЧњЯпLЕФаЮзДЪЧ________ЃЎ
бщжЄЃК
ЃЈ4ЃЉЩшЕуPЕФзјБъЪЧ![]() ЃЌИљОнЭМ1жаЯпЖЮPAгыPMЕФЙиЯЕЃЌЧѓГіyЙигкxЕФКЏЪ§НтЮіЪНЃЎ
ЃЌИљОнЭМ1жаЯпЖЮPAгыPMЕФЙиЯЕЃЌЧѓГіyЙигкxЕФКЏЪ§НтЮіЪНЃЎ
гІгУЃК
ЃЈ5ЃЉШчЭМ3ЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌЧѓЕуDЕФзнзјБъ
ЃЌЧѓЕуDЕФзнзјБъ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
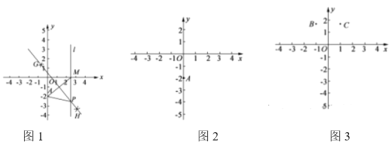
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕугыетЬѕЯпЖЮСНИіЖЫЕуЕФОрРыЯрЕШЃЛЃЈ2ЃЉЭММћНтЮіЃЌХзЮяЯпЃЛЃЈ3ЃЉМћНтЮіЃЛЃЈ4ЃЉ
ЃЌЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕугыетЬѕЯпЖЮСНИіЖЫЕуЕФОрРыЯрЕШЃЛЃЈ2ЃЉЭММћНтЮіЃЌХзЮяЯпЃЛЃЈ3ЃЉМћНтЮіЃЛЃЈ4ЃЉ![]() ЃЛЃЈ5ЃЉ
ЃЛЃЈ5ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩГпЙцзїЭМЕФВНжшПЩжЊЃЌHGЪЧAMЕФжаДЙЯпЃЌНсКЯжаДЙЯпЕФаджЪЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉИљОнЕкЃЈ1ЃЉЕФзїЭМЗНЗЈЃЌЕУЕНЯргІЕуPЕФЮЛжУЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉгУЦНЛЌЕФЧњЯпзїГіЭМЯѓЃЌМДПЩЃЛ
ЃЈ4ЃЉЙ§ЕуPзї![]() жсгкЕуEЃЌгУКЌxЃЌyЕФДњЪ§ЪНБэЪО
жсгкЕуEЃЌгУКЌxЃЌyЕФДњЪ§ЪНБэЪО![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНсКЯЙДЙЩЖЈРэЃЌМДПЩЕУЕНД№АИЃЛ
ЃЌНсКЯЙДЙЩЖЈРэЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ5ЃЉСЌНг![]() ЃЌгЩЬтвтЕУЕБ
ЃЌгЩЬтвтЕУЕБ![]() ЪБЃЌдк
ЪБЃЌдк![]() ЕФЭтНгдВЩЯЃЌЛЁ
ЕФЭтНгдВЩЯЃЌЛЁ![]() ЫљЖдЕФдВаФНЧЮЊ60ЁуЃЌ
ЫљЖдЕФдВаФНЧЮЊ60ЁуЃЌ![]() ЕФЭтНгдВдВаФЮЊзјБъдЕуOЃЌЩш
ЕФЭтНгдВдВаФЮЊзјБъдЕуOЃЌЩш![]() ЃЌЧѓГіbЕФжЕЃЌНјЖјМДПЩЧѓНтЃЎ
ЃЌЧѓГіbЕФжЕЃЌНјЖјМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉ![]() ЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕугыетЬѕЯпЖЮСНИіЖЫЕуЕФОрРыЯрЕШ
ЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕугыетЬѕЯпЖЮСНИіЖЫЕуЕФОрРыЯрЕШ
ЃЈ2ЃЉ
MЕФзјБъ | Ё |
|
|
|
| Ё |
PЕФзјБъ | Ё |
|
|
|
| Ё |
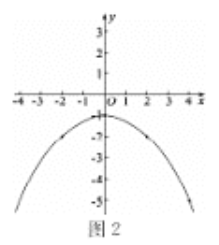
ЃЈ3ЃЉВнЭММћЭМ2ЃКаЮзДЃКХзЮяЯп
ЃЈ4ЃЉШчЭМ1ЃЌЙ§ЕуPзї![]() жсгкЕуEЃЌ
жсгкЕуEЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
дк![]() жаЃЌ
жаЃЌ![]()
МД![]()
ЛЏМђЃЌЕУ![]()
ЁрyЙигкxЕФКЏЪ§НтЮіЪНЮЊ![]() ЃЎ
ЃЎ
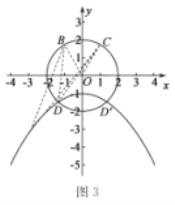
ЃЈ5ЃЉСЌНг![]() ЃЌвзЕУ
ЃЌвзЕУ![]() ЃЌгж
ЃЌгж![]()
Ёр![]() ЮЊЕШБпШ§НЧаЮЃЌЁр
ЮЊЕШБпШ§НЧаЮЃЌЁр![]()
ЕБ![]() ЪБЃЌдк
ЪБЃЌдк![]() ЕФЭтНгдВЩЯЃЌЛЁ
ЕФЭтНгдВЩЯЃЌЛЁ![]() ЫљЖдЕФдВаФНЧЮЊ60Ёу
ЫљЖдЕФдВаФНЧЮЊ60Ёу
ЦфдВаФдк![]() ЕФДЙжБЦНЗжЯпyжсЩЯЃЌ
ЕФДЙжБЦНЗжЯпyжсЩЯЃЌ
Ёр![]() ЕФЭтНгдВдВаФЮЊзјБъдЕуOЃЌ
ЕФЭтНгдВдВаФЮЊзјБъдЕуOЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌМД
ЃЌМД![]() Ђй
Ђй
гжЕуDдкИУХзЮяЯпЩЯ
Ёр![]() Ђк
Ђк
гЩЂйЂкСЊСЂНтЕУЃК![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
Ъ§аЮНсКЯПЩЕУЃЌ
ЕБ![]() ЪБЃЌЕуDЕФзнзјБъ
ЪБЃЌЕуDЕФзнзјБъ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ
![]()


 ГхДЬ100Зж1КХОэЯЕСаД№АИ
ГхДЬ100Зж1КХОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЕижЎМфЪЧвЛЬѕжБТЗЃЌдкШЋУёНЁЩэЛюЖЏжаЃЌедУїбєХмВНДгМзЕиЭљввЕиЃЌЭѕКЦдТЦяздааГЕДгввЕиЭљМзЕиЃЌСНШЫЭЌЪБГіЗЂЃЌЭѕКЦдТЯШЕНДяФПЕФЕиЃЌСНШЫжЎМфЕФОрРы![]() гыдЫЖЏЪБМф
гыдЫЖЏЪБМф![]() ЕФКЏЪ§ЙиЯЕДѓжТШчЭМЫљЪОЃЌЯТСаЫЕЗЈжаДэЮѓЕФЪЧЃЈ ЃЉЃЎ
ЕФКЏЪ§ЙиЯЕДѓжТШчЭМЫљЪОЃЌЯТСаЫЕЗЈжаДэЮѓЕФЪЧЃЈ ЃЉЃЎ
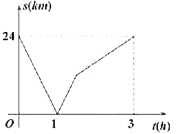
A.СНШЫГіЗЂ1аЁЪБКѓЯргіB.едУїбєХмВНЕФЫйЖШЮЊ![]()
C.ЭѕКЦдТЕНДяФПЕФЕиЪБСНШЫЯрОр![]() D.ЭѕКЦдТБШедУїбєЬсЧА
D.ЭѕКЦдТБШедУїбєЬсЧА![]() ЕНФПЕФЕи
ЕНФПЕФЕи
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=3ЃЌBC=4ЃЌЖЏЕуPДгAЕуГіЗЂЃЌАДAЁњBЁњCЕФЗНЯђдкABКЭBCЩЯвЦЖЏЃЌМЧPA=xЃЌЕуDЕНжБЯпPAЕФОрРыЮЊyЃЌдђyЙигкxЕФКЏЪ§ЭМЯѓДѓжТЪЧЃЈ ЃЉ

A. B.
B.
C. D.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСвдЯТВФСЯЃЌВЂНтОіЯргІЮЪЬтЃК
аЁУїдкПЮЭтбЇЯАЪБгіЕНетбљвЛИіЮЪЬтЃК
ЖЈвхЃКШчЙћЖўДЮКЏЪ§yЃНa1x2+b1x+c1ЃЈa1Ёй0ЃЌa1ЁЂb1ЁЂc1ЪЧГЃЪ§ЃЉгыyЃНa2x2+b2x+c2ЃЈa2Ёй0ЃЌa2ЁЂb2ЁЂc2ЪЧГЃЪ§ЃЉТњзуa1+a2ЃН0ЃЌb1ЃНb2ЃЌc1+c2ЃН0ЃЌдђетСНИіКЏЪ§ЛЅЮЊЁАа§зЊКЏЪ§ЁБЃЎЧѓКЏЪ§yЃН2x2Љ3x+1ЕФа§зЊКЏЪ§ЃЌаЁУїЪЧетбљЫМПМЕФЃЌгЩКЏЪ§yЃН2x2Љ3x+1ПЩжЊЃЌa1ЃН2ЃЌb1ЃНЉ3ЃЌc1ЃН1ЃЌИљОнa1+a2ЃН0ЃЌb1ЃНb2ЃЌc1+c2ЃН0ЃЌЧѓГіa2ЃЌb2ЃЌc2ОЭФмШЗЖЈетИіКЏЪ§ЕФа§зЊКЏЪ§ЃЎ
ЧыЫМПМаЁУїЕФЗНЗЈНтОіЯТУцЮЪЬтЃК
ЃЈ1ЃЉаДГіКЏЪ§yЃНx2Љ4x+3ЕФа§зЊКЏЪ§ЃЎ
ЃЈ2ЃЉШєКЏЪ§yЃН5x2+ЃЈmЉ1ЃЉx+nгыyЃНЉ5x2ЉnxЉ3ЛЅЮЊа§зЊКЏЪ§ЃЌЧѓЃЈm+nЃЉ2020ЕФжЕЃЎ
ЃЈ3ЃЉвбжЊКЏЪ§yЃН2ЃЈxЉ1ЃЉЃЈx+3ЃЉЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуAЁЂBЁЂCЙигкдЕуЕФЖдГЦЕуЗжБ№ЪЧA1ЁЂB1ЁЂC1ЃЌЪдЧѓжЄЃКОЙ§ЕуA1ЁЂB1ЁЂC1ЕФЖўДЮКЏЪ§гыyЃН2ЃЈxЉ1ЃЉЃЈx+3ЃЉЛЅЮЊЁАа§зЊКЏЪ§ЁБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
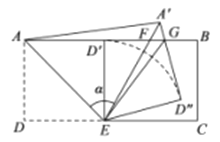
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌАбЁїEADбиAEелЕўЃЌЪЙЕуDЧЁКУТфдкABБпЩЯЕФ
ЃЌАбЁїEADбиAEелЕўЃЌЪЙЕуDЧЁКУТфдкABБпЩЯЕФ![]() ДІЃЌдйНЋ
ДІЃЌдйНЋ![]() ШЦЕуEЫГЪБеыа§зЊ
ШЦЕуEЫГЪБеыа§зЊ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЧЁКУОЙ§
ЧЁКУОЙ§![]() ЕФжаЕуFЃЎ
ЕФжаЕуFЃЎ![]() НЛABгкЕуGЃЌСЌНг
НЛABгкЕуGЃЌСЌНг![]() гаШчЯТНсТлЃКЂй
гаШчЯТНсТлЃКЂй![]() ЕФГЄЖШЪЧ
ЕФГЄЖШЪЧ![]() ЃЛЂкЛЁ
ЃЛЂкЛЁ![]() ЕФГЄЖШЪЧ
ЕФГЄЖШЪЧ![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЎЩЯЪіНсТлжаЃЌЫљгае§ШЗЕФађКХЪЧ________ЃЎ
ЃЎЩЯЪіНсТлжаЃЌЫљгае§ШЗЕФађКХЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЪЧШёНЧШ§НЧаЮ
ЪЧШёНЧШ§НЧаЮ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧыдкЭМ1жагУЮоПЬЖШЕФжБГпКЭдВЙцзїЭМЃЛзїжБЯп![]() ЃЌЪЙ
ЃЌЪЙ![]() ЩЯЕФИїЕуЕН
ЩЯЕФИїЕуЕН![]() ЁЂ
ЁЂ![]() СНЕуЕФОрРыЯрЕШЃЛЩшжБЯп
СНЕуЕФОрРыЯрЕШЃЛЩшжБЯп![]() гы
гы![]() ЁЂ
ЁЂ![]() ЗжБ№НЛгкЕу
ЗжБ№НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌзївЛИідВЃЌЪЙЕУдВаФ
ЃЌзївЛИідВЃЌЪЙЕУдВаФ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЧвгыБп
ЩЯЃЌЧвгыБп![]() ЁЂ
ЁЂ![]() ЯрЧаЃЛЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉ
ЯрЧаЃЛЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФАыОЖЮЊ________ЃЎ
ЕФАыОЖЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDФкНггкЁбOЃЌABЪЧЁбOЕФжБОЖЃЌЕуPдкCAЕФбгГЄЯпЩЯЃЌЁЯCAD=45Ёу.

(1)ШєAB=4ЃЌЧѓЛЁCDЕФГЄ.
(2)ШєЛЁBC=ЛЁADЃЌAD=AP. ЧѓжЄЃКPDЪЧЁбOЕФЧаЯп.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ,вдACЮЊжБОЖЕФАыдВOНЛгкЕуDЃЌЙ§ЕуDзїдВOЕФЧаЯпЃЌНЛBCгкЕуEЃЌЕуFЪЧАыдВЩЯвьгкЕуDЕФШЮвЛЖЏЕуЃЎ
,вдACЮЊжБОЖЕФАыдВOНЛгкЕуDЃЌЙ§ЕуDзїдВOЕФЧаЯпЃЌНЛBCгкЕуEЃЌЕуFЪЧАыдВЩЯвьгкЕуDЕФШЮвЛЖЏЕуЃЎ
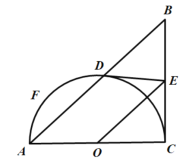
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЬюПеЃК
ЂйШє![]() ЃЌдђЫФБпаЮ
ЃЌдђЫФБпаЮ![]() ЕФУцЛ§ЮЊ________ЃЛ
ЕФУцЛ§ЮЊ________ЃЛ
ЂкЕБ![]() ЕФЖШЪ§ЪЧ_______ЪБЃЌвд
ЕФЖШЪ§ЪЧ_______ЪБЃЌвд![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЎ
ЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГМвЕчЯњЪлЩЬГЧЕчБљЯфЕФЯњЪлМлЮЊУПЬЈ2100дЊЃЌПеЕїЕФЯњЪлМлЮЊУПЬЈ1750дЊЃЌУПЬЈЕчБљЯфЕФНјМлБШУПЬЈПеЕїЕФНјМлЖр400дЊЃЌЩЬГЧгУ80000дЊЙКНјЕчБљЯфЕФЪ§СПгыгУ64000дЊЙКНјПеЕїЕФЪ§СПЯрЕШЃЎ
ЧѓУПЬЈЕчБљЯфгыПеЕїЕФНјМлЗжБ№ЪЧЖрЩйЃП
ЃЈ2ЃЉЯждкЩЬГЧзМБИвЛДЮЙКНјетСНжжМвЕчЙВ100ЬЈЃЌЩшЙКНјЕчБљЯфxЬЈЃЌет100ЬЈМвЕчЕФЯњЪлзмРћШѓЮЊyдЊЃЌвЊЧѓЙКНјПеЕїЪ§СПВЛГЌЙ§ЕчБљЯфЪ§СПЕФ2БЖЃЌзмРћШѓВЛЕЭгк13000дЊЃЌЧыЗжЮіКЯРэЕФЗНАИЙВгаЖрЩйжжЃПВЂШЗЖЈЛёРћзюДѓЕФЗНАИвдМАзюДѓРћШѓ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com