
【题目】在![]() 中,
中,![]() ,以AC为直径的半圆O交于点D,过点D作圆O的切线,交BC于点E,点F是半圆上异于点D的任一动点.
,以AC为直径的半圆O交于点D,过点D作圆O的切线,交BC于点E,点F是半圆上异于点D的任一动点.
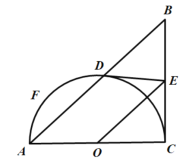
(1)求证:![]() ;
;
(2)填空:
①若![]() ,则四边形
,则四边形![]() 的面积为________;
的面积为________;
②当![]() 的度数是_______时,以
的度数是_______时,以![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.
【答案】(1)见解析;(2)①![]() ;②30°或60°.
;②30°或60°.
【解析】
(1)连接OD,证明![]() ,得
,得![]() ,利用外角和定理得
,利用外角和定理得![]() ,可得
,可得![]() ,证得平行;
,证得平行;
(2)①连接CD,证明![]() ,求出AC,用勾股定理求出CD,结合
,求出AC,用勾股定理求出CD,结合![]() ,E为中点,四边形
,E为中点,四边形![]() 在BD上的高为CD的一半,可求出面积;
在BD上的高为CD的一半,可求出面积;
②分为点F在![]() 和
和![]() 上,根据菱形的性质结合圆的特点,分类讨论即可.
上,根据菱形的性质结合圆的特点,分类讨论即可.
(1)连接DO,则![]()
因为DE是圆的切线,所以![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
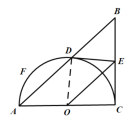
(2) ①连接CD,如图所示:
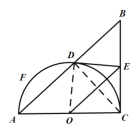
∵AC为直径
∴![]() °
°
∵![]() 且
且![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() 且E为中点
且E为中点
∴![]()
故答案为:![]()
②若点F在![]() 上时,如图所示:
上时,如图所示:
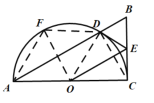
∵AODF为菱形
∴AF=AO
∵AO=OF
∴![]() 为等边三角形
为等边三角形
∴![]()
∴![]()
∴![]()
若点F在![]() 上,作图如下:
上,作图如下:
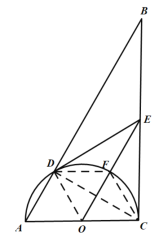
∵AODF为菱形
∴AD=AO
∵AO=OD
∴![]() 为等边三角形
为等边三角形
∴![]()
∴![]()
故答案为:30°或60°


科目:初中数学 来源: 题型:
【题目】某商店计划一次性购进甲、乙两种商品共![]() 件,甲、乙两种商品的进价和售价如下表所示:
件,甲、乙两种商品的进价和售价如下表所示:
甲 | 乙 | |
进价(元/件) | 100 | 80 |
售价(元/件) | 150 | 120 |
设购进甲种商品的数量为![]() 件.
件.
(1)设进货成本为![]() 元,求
元,求![]() 与
与![]() 之间的函数解析式;若购进甲种商品的数量不少于
之间的函数解析式;若购进甲种商品的数量不少于![]() 件,则最低进货成本是多少元?
件,则最低进货成本是多少元?
(2)若除了进货成本,还要支付运费和销售员工工资共![]() 元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价
元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价![]() 元
元![]() ,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为
,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为![]() 元.
元.
①每件甲种商品的利润是 元(用含![]() 的代数式表示)
的代数式表示)
②求![]() 关于
关于![]() 的函数解析式
的函数解析式
③当![]() 时,请你根据
时,请你根据![]() 的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
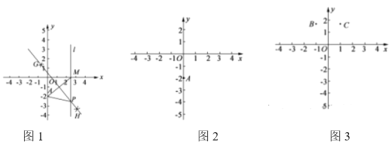
【题目】如图1,在平面直角坐标系中,点A的坐标是![]() ,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于
,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于![]() 的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为________,其理由为:________________.
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
M的坐标 | … |
|
|
|
| … |
P的坐标 | … |
|
| … |
猜想:
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线L,猜想曲线L的形状是________.
验证:
(4)设点P的坐标是![]() ,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
(5)如图3,点![]() ,
,![]() ,求点D的纵坐标
,求点D的纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程![]() 与它们的行驶时间
与它们的行驶时间![]() 之间的函数关系.小欣同学结合图像得出如下结论:
之间的函数关系.小欣同学结合图像得出如下结论:
①快车途中停留了![]() ; ②快车速度比慢车速度多
; ②快车速度比慢车速度多![]() ;
;
③图中![]() ; ④快车先到达目的地.
; ④快车先到达目的地.
其中正确的是( )

A.①③B.②③C.②④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,把与
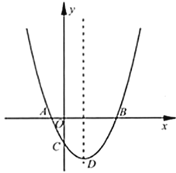
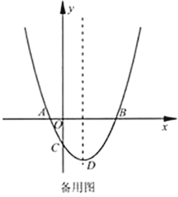
中,把与![]() 轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线
轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线![]() 的顶点为
的顶点为![]() ,交
,交![]() 轴于点
轴于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 左侧),交
左侧),交![]() 轴于点
轴于点![]() .抛物线
.抛物线![]() 与
与![]() 是“共根抛物线”,其顶点为
是“共根抛物线”,其顶点为![]() .
.
(1)若抛物线![]() 经过点
经过点![]() ,求
,求![]() 对应的函数表达式;
对应的函数表达式;
(2)当![]() 的值最大时,求点
的值最大时,求点![]() 的坐标;
的坐标;
(3)设点![]() 是抛物线
是抛物线![]() 上的一个动点,且位于其对称轴的右侧.若
上的一个动点,且位于其对称轴的右侧.若![]() 与
与![]() 相似,求其“共根抛物线”
相似,求其“共根抛物线”![]() 的顶点
的顶点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 交
交![]() 轴于点A,交
轴于点A,交![]() 轴于点B,抛物线
轴于点B,抛物线![]() 经过点A,交
经过点A,交![]() 轴于点
轴于点![]() ,点P为直线AB下方抛物线上一动点,过点P作
,点P为直线AB下方抛物线上一动点,过点P作![]() 于D,连接AP.
于D,连接AP.
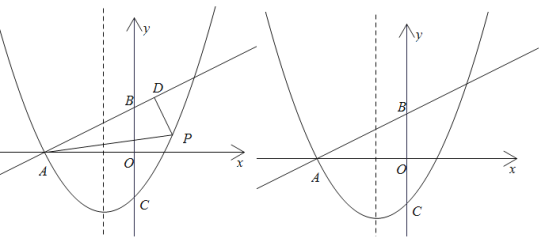
(1)求抛物线的解析式;
(2)若以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点P的坐标;
相似,求点P的坐标;
(3)将![]() 绕点A旋转,当点O的对应点
绕点A旋转,当点O的对应点![]() 落在抛物线的对称轴上时,请直接写出点B的对应点
落在抛物线的对称轴上时,请直接写出点B的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
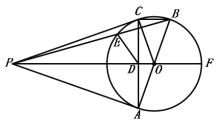
【题目】如图,⊙![]() 是△
是△![]() 的外接圆,
的外接圆,![]() 为直径,点
为直径,点![]() 是⊙
是⊙![]() 外一点,且
外一点,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() .
.
⑴.证明:![]() =
=![]() ;
;
⑵.若![]() ,证明:
,证明:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑶.在⑵的条件下,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ;若
;若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有 名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com