
【题目】如图,⊙![]() 是△
是△![]() 的外接圆,
的外接圆,![]() 为直径,点
为直径,点![]() 是⊙
是⊙![]() 外一点,且
外一点,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() .
.
⑴.证明:![]() =
=![]() ;
;
⑵.若![]() ,证明:
,证明:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑶.在⑵的条件下,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ;若
;若![]() ,求
,求![]() 的长.
的长.
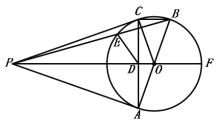
【答案】(1)证明过程见解析;(2)证明过程见解析;(3)![]()
【解析】
(1)连接CO,易证△PCO≌△PAO,得PO为∠APC的角平分线,根据条件证出F为优弧![]() 中点,即可证明
中点,即可证明![]() =
=![]() ;
;
(2)因为AB是直径,所以∠ACB=90°,由tan∠ABC=![]() 可求得∠ABC的正弦和余弦,设⊙O的半径为r,则AB=2r,根据三角函数表示出BC,AC的长度,由勾股定理表示出OD的长度,易得PA=PC=
可求得∠ABC的正弦和余弦,设⊙O的半径为r,则AB=2r,根据三角函数表示出BC,AC的长度,由勾股定理表示出OD的长度,易得PA=PC=![]() ,
,![]() ,PO=PD+OD=3r,由
,PO=PD+OD=3r,由![]() 可得PA⊥OA,即可证明
可得PA⊥OA,即可证明![]() 是⊙
是⊙![]() 的切线;
的切线;
(3)连接AE,过E作EN⊥PD于N,过B作BH⊥PF于H,由(2)可得,![]() ,PB=
,PB=![]() ,证出△PEA∽△PAB,可得
,证出△PEA∽△PAB,可得![]() ,证出四边形BCDH是矩形,得BH=CD=
,证出四边形BCDH是矩形,得BH=CD=![]() ,在Rt△BPH和Rt△PEN中表示出sin∠BPH,可得
,在Rt△BPH和Rt△PEN中表示出sin∠BPH,可得![]() ,
,![]() ,ND=PD-PN=
,ND=PD-PN=![]() ,在Rt△NED中,DE=
,在Rt△NED中,DE=![]() ,代入r=3即可
,代入r=3即可
解:(1)证明:如图,连接CO,
在△PCO和△PAO中,
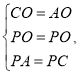
∴△PCO≌△PAO(SSS),
∴∠CPO=∠APO,即PO为∠APC的角平分线,
∵PA=PC,
∴CD=AD,PF⊥AC,
∵AC为⊙O的弦,PF过圆心O,
∴F为优弧![]() 中点,
中点,
∴![]() =
=![]() ,
,
(2)证明:∵AB是⊙O的直径,且弦AB所对圆周角为∠ACB,
∴∠ACB=90°,
∵tan∠ABC=![]() ,
,
∴sin∠ABC=![]() ,cos∠ABC=
,cos∠ABC=![]() ,
,
设⊙O的半径为r,则AB=2r,
∴BC=ABcos∠ABC=![]() ,AC=ABsin∠ABC=
,AC=ABsin∠ABC=![]() ,
,
∴![]() ,
,
∵PA=PC=![]() AB,
AB,
∴PA=PC=![]() ,
,
∴![]() ,
,
∴PO=PD+OD=3r,
∴![]() ,即PA⊥OA,
,即PA⊥OA,
又∵OA是⊙O半径,
∴PA是⊙O的切线;
(3)由(2)可得![]() ,
,
∴![]() ,
,
在Rt△PBA中,![]() ,连接AE,可得∠AEB=90°,
,连接AE,可得∠AEB=90°,
∴∠PEA=∠PAB=90°,又∠APE=∠APB,
∴△PEA∽△PAB,
∴![]() ,
,
∴![]() ,
,
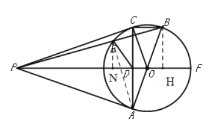
过E作EN⊥PD于N,过B作BH⊥PF于H,如图所示,
∴∠BCD=∠CDF=∠BHD=90°,
∴四边形BCDH是矩形,
∴BH=CD=![]() ,
,
在Rt△BPH中,sin∠BPH=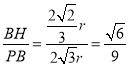 ,
,
在Rt△PEN中,sin∠BPH=![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴ND=PD-PN=![]() ,
,
在Rt△NED中,DE=![]() ,
,
∵![]() ,
,
∴DE=![]() .
.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.

(1)若AB=4,求弧CD的长.
(2)若弧BC=弧AD,AD=AP. 求证:PD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,以AC为直径的半圆O交于点D,过点D作圆O的切线,交BC于点E,点F是半圆上异于点D的任一动点.
,以AC为直径的半圆O交于点D,过点D作圆O的切线,交BC于点E,点F是半圆上异于点D的任一动点.
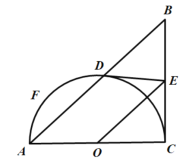
(1)求证:![]() ;
;
(2)填空:
①若![]() ,则四边形
,则四边形![]() 的面积为________;
的面积为________;
②当![]() 的度数是_______时,以
的度数是_______时,以![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
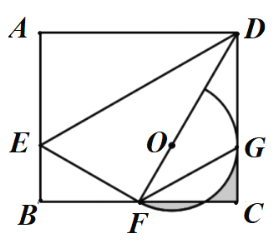
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 上的一点,连接
上的一点,连接![]() ,将△
,将△![]() 进行翻折,恰好使点
进行翻折,恰好使点![]() 落在
落在![]() 的中点
的中点![]() 处,在
处,在![]() 上取一点
上取一点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作半圆与
的长为半径作半圆与![]() 相切于点
相切于点![]() ;若
;若![]() ,则图中阴影部分的面积为 ____ .
,则图中阴影部分的面积为 ____ .
查看答案和解析>>
科目:初中数学 来源: 题型:
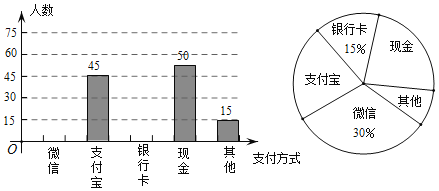
【题目】随着科技的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份“你最喜欢的支付方式”调查问卷(每人必选且只选一种),在某商场随机调查了部分顾客,并将统计结果绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人,在扇形统计图中,表示“现金”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是 ;
(3)运用这次的调查结果估计1000名顾客中用“支付宝”支付的有多少人?
(4)在一次购物中,嘉嘉和琪琪都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD,E是线段BC上一点,N是线段BC延长线上一点,以AE为边在直线BC的上方作正方形AEFG.

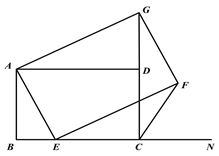
图(1) 图(2)
(1)连接GD,求证:DG=BE;
(2)连接FC,求∠FCN的度数;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=m,BC=n(m、n为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线BC的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含m、n的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请画图说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点A在
,点A在![]() 上,四边形
上,四边形![]() 是矩形,连接
是矩形,连接![]() 、
、![]() 交于点E,连接
交于点E,连接![]() 交
交![]() 于点F.下列4个判断:①
于点F.下列4个判断:①![]() 平分
平分![]() ;②
;②![]() ;③
;③![]() ;④若点G是线段
;④若点G是线段![]() 的中点,则
的中点,则![]() 为等腰直角三角形.正确判断的个数是( )
为等腰直角三角形.正确判断的个数是( )

A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com