
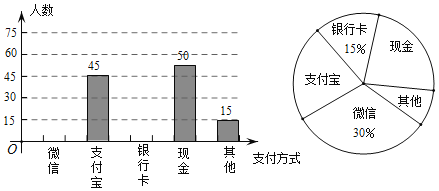
【题目】随着科技的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份“你最喜欢的支付方式”调查问卷(每人必选且只选一种),在某商场随机调查了部分顾客,并将统计结果绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人,在扇形统计图中,表示“现金”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是 ;
(3)运用这次的调查结果估计1000名顾客中用“支付宝”支付的有多少人?
(4)在一次购物中,嘉嘉和琪琪都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
【答案】(1)200,90°;(2)见解析,微信;(3)225人;(4)![]()
【解析】
(1)用支付宝、现金及其他的人数和除以这三者的百分比之和可得总人数,再用![]() 乘以“现金”人数所占的百分比即可得圆心角的度数;
乘以“现金”人数所占的百分比即可得圆心角的度数;
(2)用总人数乘以微信、银行卡对应的百分比可得微信、银行卡的人数,从而补全条形统计图,再根据众数的定义求解可得支付方式的众数;
(3)用总人数乘以支付宝对应的百分比可得“支付宝”的人数;
(4)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人恰好选择同一种支付方式的情况,再利用概率公式即可求得答案.
解:(1)这次活动共调查了![]() (人
(人![]() ,
,
在扇形统计图中,表示“现金”支付的扇形圆心角的度数为![]() ,
,
故答案为:200,![]() ;
;
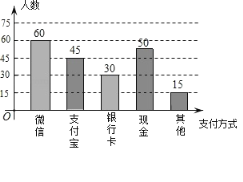
(2)微信人数为200×30%=60人,银行卡人数为200×15%=30人.
补全图形如下图,
由条形统计图可知,选择微信支付的人数有60人,最多,所以支付方式的“众数”是“微信”;
(3)1000×![]() =225(人).
=225(人).
(4)将微信记为A,支付宝记为B,银行卡记为C,画树状图如图,
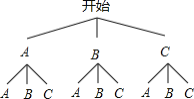
∵共有9种等可能的结果,其中两人恰好选择同一种支付方式的有3种,
∴两人恰好选择同一种支付方式的概率为![]() =
=![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】2019年全国两会于3月5日在人民大会堂开幕,某社区为了解居民对此次两会的关注程度,在全社区范围内随机抽取部分居民进行问卷调查,根据调查结果,把居民对两会的关注程度分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下不完整的统计图:
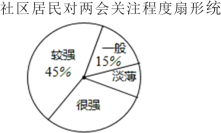
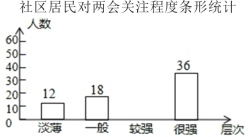
请结合图表中的信息,解答下列问题:
(1)此次调查一共随机抽取了_____名居民;
(2)请将条形统计图补充完整;
(3)扇形统计图中,“很强”所对应扇形圆心角的度数为_____;
(4)若该社区有1500人,则可以估计该社区居民对两会的关注程度为“淡薄”层次的约有 _____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程![]() 与它们的行驶时间
与它们的行驶时间![]() 之间的函数关系.小欣同学结合图像得出如下结论:
之间的函数关系.小欣同学结合图像得出如下结论:
①快车途中停留了![]() ; ②快车速度比慢车速度多
; ②快车速度比慢车速度多![]() ;
;
③图中![]() ; ④快车先到达目的地.
; ④快车先到达目的地.
其中正确的是( )

A.①③B.②③C.②④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 交
交![]() 轴于点A,交
轴于点A,交![]() 轴于点B,抛物线
轴于点B,抛物线![]() 经过点A,交
经过点A,交![]() 轴于点
轴于点![]() ,点P为直线AB下方抛物线上一动点,过点P作
,点P为直线AB下方抛物线上一动点,过点P作![]() 于D,连接AP.
于D,连接AP.
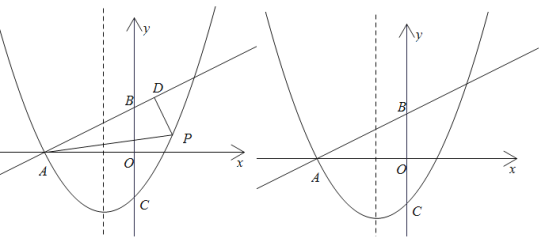
(1)求抛物线的解析式;
(2)若以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点P的坐标;
相似,求点P的坐标;
(3)将![]() 绕点A旋转,当点O的对应点
绕点A旋转,当点O的对应点![]() 落在抛物线的对称轴上时,请直接写出点B的对应点
落在抛物线的对称轴上时,请直接写出点B的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
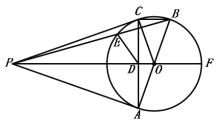
【题目】如图,⊙![]() 是△
是△![]() 的外接圆,
的外接圆,![]() 为直径,点
为直径,点![]() 是⊙
是⊙![]() 外一点,且
外一点,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() .
.
⑴.证明:![]() =
=![]() ;
;
⑵.若![]() ,证明:
,证明:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑶.在⑵的条件下,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ;若
;若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
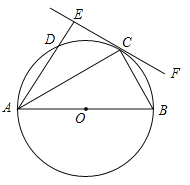
【题目】如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧![]() 的长l.
的长l.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有 名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
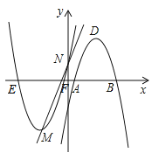
【题目】如图,在平面直角坐标系中,已知抛物线![]() :
:![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,先将抛物线
,先将抛物线![]() 沿
沿![]() 轴翻折,再向右平移p个单位长度后得到抛物
轴翻折,再向右平移p个单位长度后得到抛物![]() ,直线
,直线![]() ;
;![]() 经过
经过![]() ,
,![]() 两点.
两点.
(1)求点![]() 的坐标,并结合图象直接写出不等式:
的坐标,并结合图象直接写出不等式:![]() 的解集;
的解集;
(2)若抛物线![]() 的顶点
的顶点![]() 与点
与点![]() 关于原点对称,求p的值及抛物线
关于原点对称,求p的值及抛物线![]() 的解析式;
的解析式;
(3)若抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() 、
、![]() (点
(点![]() 、
、![]() 分别与抛物线
分别与抛物线![]() 上点
上点![]() 、
、![]() 对应),试问四边形
对应),试问四边形![]() 是何种特殊四边形?并说明其理由.
是何种特殊四边形?并说明其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
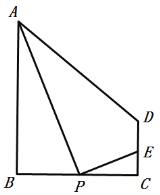
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .P为线段
.P为线段![]() 上的一动点,且和B、C不重合,连接
上的一动点,且和B、C不重合,连接![]() ,过点P作
,过点P作![]() 交射线
交射线![]() 于点E.
于点E.
聪聪根据学习函数的经验,对这个问题进行了研究:
(1)通过推理,他发现![]() ,请你帮他完成证明.
,请你帮他完成证明.
(2)利用几何画板,他改变![]() 的长度,运动点P,得到不同位置时,
的长度,运动点P,得到不同位置时,![]() 、
、![]() 的长度的对应值:
的长度的对应值:
当![]() 时,得表1:
时,得表1:
| … | 1 | 2 | 3 | 4 | 5 | … |
| … | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | … |
当![]() 时,得表2:
时,得表2:
| … | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| … | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | … |
这说明,点P在线段![]() 上运动时,要保证点E总在线段
上运动时,要保证点E总在线段![]() 上,
上,![]() 的长度应有一定的限制.
的长度应有一定的限制.
①填空:根据函数的定义,我们可以确定,在![]() 和
和![]() 的长度这两个变量中,_____的长度为自变量,_____的长度为因变量;
的长度这两个变量中,_____的长度为自变量,_____的长度为因变量;
②设![]() ,当点P在线段
,当点P在线段![]() 上运动时,点E总在线段
上运动时,点E总在线段![]() 上,求m的取值范围.
上,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com