练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆，交弦AB于点D，连接CD，则阴影部分的面积为（　　）

    A．π﹣1 B．2π﹣1      C．π﹣1     D．π﹣2


    A【考点】扇形面积的计算．

    【分析】已知BC为直径，则∠CDB=90°，在等腰直角三角形ABC中，CD垂直平分AB，CD=DB，D为半圆的中点，阴影部分的面积可以看做是扇形ACB的面积与△ADC的面积之差．

    【解答】解：在Rt△ACB中，AB==2，

    ∵BC是半圆的直径，

    ∴∠CDB=90°，

    在等腰Rt△ACB中，CD垂直平分AB，CD=BD=，

    ∴D为半圆的中点，

    S阴影部分=S扇形ACB﹣S△ADC=π×22﹣×（）2=π﹣1．

    故选A．

    【点评】本题主要考查扇形面积的计算，不规则图形面积的求法，熟记扇形的面积公式是解答此题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列运算中正确的是（　　）

    A．a2+a3=a5   B．a2•a4=a8    C．a6÷a2=a3   D．（a2）3=a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠ACB=90°，∠B=40°，D为线段AB的中点，则∠ACD=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知反比例函数y=的图象的一支位于第一象限．

    （1）判断该函数图象的另一支所在的象限，并求m的取值范围；

    （2）如图，O为坐标原点，点A在该反比例函数位于第一象限的图象上，点B与点A关于x轴对称，若△OAB的面积为6，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，∠B=90°，BC=2AB，则cosA=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图①，将▱ABCD置于直角坐标系中，其中BC边在x轴上（B在C的左边），点D坐标为（0，4），直线MN：y=x﹣6沿着x轴的负方向以每秒1个单位的长度平移，设在平移过程中该直线被▱ABCD截得的线段长度为m，平移时间为t，m与t的函数图象如图②所示．

    （1）填空：点C的坐标为　 　；在平移过程中，该直线先经过B、D中的哪一点？　 　；（填“B”或“D”）

    （2）点B的坐标为　 　，n=　 　，a=　 　；

    （3）在平移过程中，求该直线扫过▱ABCD的面积y与t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


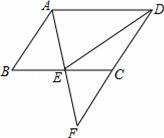
    如图，在▱ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．

    （1）试说明：AB=CF；

    （2）连接DE，若AD=2AB，试说明：DE⊥AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，则这个几何体的左视图为（　　）

    A．   B．    C．   D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：﹣22﹣（﹣2）2+|﹣5|+2cos30°﹣（）﹣1+（9﹣）0+．

    查看答案和解析>>

    同步练习册答案