
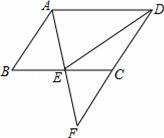
如图,在▱ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)试说明:AB=CF;
(2)连接DE,若AD=2AB,试说明:DE⊥AF.

【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】证明题.
【分析】(1)由在▱ABCD中,E是BC的中点,利用ASA,即可判定△ABE≌△FCE,继而证得结论;
(2)由AD=2AB,AB=FC=CD,可得AD=DF,又由△ABE≌△FCE,可得AE=EF,然后利用三线合一,证得结论.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABE=∠FCE,
∵E为BC中点,
∴BE=CE,
在△ABE与△FCE中,
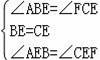
 ,
,
∴△ABE≌△FCE(ASA),
∴AB=FC;
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF,
∵△ABE≌△FCE,
∴AE=EF,
∴DE⊥AF.
【点评】此题考查了平行四边形的性质、全等三角形的判定与性质以及等腰三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )


A.π﹣1 B.2π﹣1 C.
 π﹣1 D.
π﹣1 D.
 π﹣2
π﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
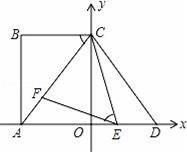
如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=
 ,∠CDE=∠CAO,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,∠CDE=∠CAO,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)求AC的长和点D的坐标;
(2)证明:△AEF∽△DCE;
(3)当△EFC为等腰三角形时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD.当∠DOA=∠OBA时,直线CD的解析式为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于F,当∠BED=120°时,求∠EFD的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题正确的个数是( )
(1)直径是圆中最大的弦.
(2)长度相等的两条弧一定是等弧.
(3)半径相等的两个圆是等圆.
(4)面积相等的两个圆是等圆.
(5)同一条弦所对的两条弧一定是等弧.
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com