
【题目】在一个箱子中有三个分别标有数字1,2,3的材质、大小都相同的小球,从中任意摸出一个小球,记下小球的数字x后,放回箱中并摇匀,再摸出一个小球,又记下小球的数字y。以先后记下的两个数字(x,y)作为点P的坐标。
(1)求点P的横坐标与纵坐标的和为4的概率,并画出树状图或列表;
(2)求点P落在以坐标原点为圆心、![]() 为半径的圆的内部的概率。
为半径的圆的内部的概率。
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
试题分析:(1)首先根据题意列出表格,然后根据表格即可求得点M坐标的所有可能的结果,然后利用概率公式解即可;
(2)确定满足条件的点的个数,利用概率公式求解,即可求得答案.
试题解析:(1)列表得:
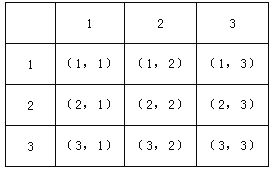
则点M坐标的所有可能的结果有九个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、
(2,3)、(3,1)、(3,2)、(3,3),和为4的有3种,
故P(和为4)= ![]() =
=![]() .
.
(2)因为点M在以坐标原点为圆心,以![]() 为半径的圆的内部,
为半径的圆的内部,
所以x2+y2<10,这样的点M有4种形式:(1,1)、(1,2)、(2,1)、(2,2),
所以点M在以坐标原点为圆心,以![]() 为半径的圆的内部的概率P=
为半径的圆的内部的概率P=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某文具店第一次用400元购进胶皮笔记本若干个,第二次又用400元购进该种型号的笔记本,但这次每个的进价是第一次进价的1.25倍,购进数量比第一次少了20个.
(1)求第一次每个笔记本的进价是多少?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后后获利不低于460元,问每个笔记本至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读并补充下面推理过程:(1)
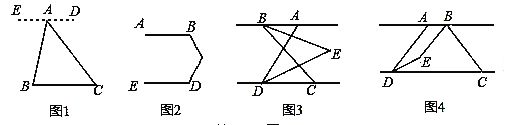
如图1,已知点A是BC外一点,连接AB,AC.
求∠BAC+∠B+∠C的度数.
解:过点A作ED∥BC,所以∠B= ,∠C= .
又因为∠EAB+∠BAC+∠DAC=180°.
所以∠B+∠BAC+∠C=180°.
方法运用:(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
深化拓展:(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
.如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
Ⅱ.如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 °.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
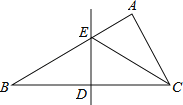
【题目】如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
A.![]() B.1 C.
B.1 C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
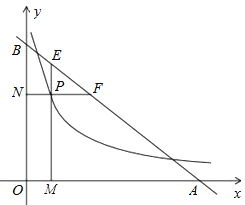
【题目】如图,直线![]() 与x轴、y轴交于A、B两点,P是反比例函数
与x轴、y轴交于A、B两点,P是反比例函数![]() 图像上位于直线下方的一点,过点P作x轴的垂线,垂足为M,交AB于点E,过点P作y轴的垂线,垂足为N,交AB于点F,则AF
图像上位于直线下方的一点,过点P作x轴的垂线,垂足为M,交AB于点E,过点P作y轴的垂线,垂足为N,交AB于点F,则AF![]() BE的值为( )
BE的值为( )
A、8 B、6 C、4 D、![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com