
已知函数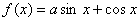 的图象经过点
的图象经过点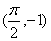 .
.
(1)求函数 的最小正周期与单调递增区间.
的最小正周期与单调递增区间.
(2)若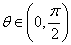 ,且
,且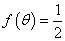 ,求
,求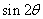 的
的 值.
值.
科目:初中数学 来源: 题型:
如图①,②,③,用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图④,⑤不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形: .

查看答案和解析>>
科目:初中数学 来源: 题型:
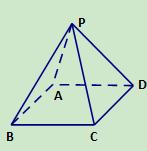
如图所示,正四棱锥 (底面是正方形,顶点在底面的射影是底面的中心)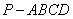 的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于
的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于
A. 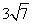 B.
B. 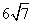 C.12 D.24
C.12 D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
已 知函数
知函数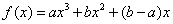 (a,b是不同时为零的常数),其导函数为
(a,b是不同时为零的常数),其导函数为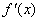 .
.
(1)当 时,若不等式
时,若不等式 对任意
对任意
 恒成立,求b的取值范围;
恒成立,求b的取值范围;
(2)若函数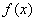 为奇函数,且在
为奇函数,且在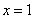 处的切线垂直于直线
处的切线垂直于直线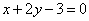 ,关于x的方程
,关于x的方程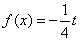 在
在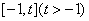 上有且只有一个实数根,求实数t的取值范围.
上有且只有一个实数根,求实数t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com