
已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
(1)证明:①当k=0时,方程为x+2=0,所以x=﹣2,方程有实数根,
②当k≠0时,∵△=(2k+1)2﹣4k×2=(2k﹣1)2≥0,即△≥0,
∴无论k取任何实数时,方程总有实数根;
(2)解:令y=0,则kx2+(2k+1)x+2=0,
解关于x的一元二次方程,得x1=﹣2,x2=﹣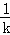 ,
,
∵二次函数的图象与x轴两个交点的横坐标均为整数,且k为正整数,
∴k=1.
∴该抛物线解析式为y=x2+3x+2,
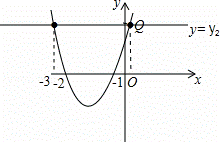 .
.
由图象得到:当y1>y2时,a>1或a<﹣3.
(3)依题意得kx2+(2k+1)x+2﹣y=0恒成立,即k(x2+2x)+x﹣y+2=0恒成立,
则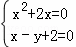 ,
,
解得 或
或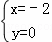 .
.
所以该抛物线恒过定点(0,2)、(﹣2,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
清明期间,某校师生组成200个小组参加“保护环境,美化家园”植树活动.综合实际情况,校方要求每小组植树量为2至5棵,活动结束后,校方随机抽查了其中50个小组,根据他们的植树量绘制出如图所示的两幅不完整统计图.请根据图中提供的信息,解答下面的问题:
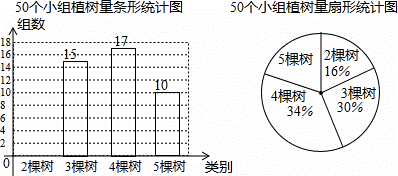
(1)请把条形统计图补充完整,并算出扇形统计图中,植树量为“5棵树”的圆心角是 72 °.
(2)请你帮学校估算此次活动共种多少棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
|
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某学校为了了解学生上学交通情况,选取九年级全体学生进行调查。根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°。已知九年级乘公交车上学的人数为50人.

(1)九年级学生中,骑自行车和乘公交车上学哪个更多?多多少人?
(2)如果全校有学生2 000人,学校准备的400个自行车停车位是否足够?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com