练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    甲、乙、丙、丁四人参加训练，近期的10次百米测试平均成绩都是13.2秒，方差如表

     选手

     甲

     乙

     丙

     丁

     方差（秒2）

     0.020

     0.019

     0.021

     0.022

    则这四人中发挥最稳定的是（　　）

    　

    A．

    甲

    B．

    乙

    C．

    丙

    D．

    丁

     


    B解：∵0.019＜0.020＜0.021＜0.022，∴乙的方差最小，

    ∴这四人中乙发挥最稳定，故选：B．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知集合，函数的定义域为集合，则

    A．         B．          C．      D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知函数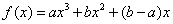（a，b是不同时为零的常数），其导函数为.

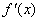    （1）当时，若不等式对任意恒成立，求b的取值范围；

    （2）若函数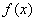为奇函数，且在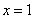处的切线垂直于直线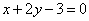，关于x的方程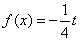在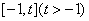上有且只有一个实数根，求实数t的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将一张边长为6cm的正方形纸片按虚线裁剪后，恰好围成底面是正六边形的棱柱，则这个六棱柱的侧面积为　　cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的方程kx2+（2k+1）x+2=0．

    （1）求证：无论k取任何实数时，方程总有实数根；

    （2）当抛物线y=kx2+（2k+1）x+2图象与x轴两个交点的横坐标均为整数，且k为正整数时，若P（a，y1），Q（1，y2）是此抛物线上的两点，且y1＞y2，请结合函数图象确定实数a的取值范围；

    （3）已知抛物线y=kx2+（2k+1）x+2恒过定点，求出定点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ）因式分解：x2﹣49=　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在⊙O的内接四边形ABCD中，点E在DC的延长线上．若∠A=50°，则∠BCE=　　．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


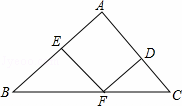
    如图，在△ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B=45°，∠C=60°．则∠EFD=（　　）

    　

    A．

    80°

    B．

    75°

    C．

    70°

    D．

    65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


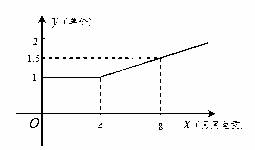
    某工厂在生产过程中每消耗1万度电可以产生产值5.5万元．电力公司规定，该工厂每月用电量不得超过16万度；月用电量不超过4万度时，单价都是1万元/万度；超过4万度时，超过部分电量单价将按用电量进行调整，电价y与月用电量x的函数关系可以用如图来表示．（效益＝产值－用电量×电价）；
    （1）设工厂的月效益为z（万元），写出z与月用电量x（万度）之间的函数关系式，并写出自变量的取值范围；
    （2）求工厂最大月效益．

     

    【

    查看答案和解析>>

    同步练习册答案