
 在△ABC中,∠BAC=90°,AB=AC,D为BC中点,且AE=CF.求证:△AED≌△CFD.
在△ABC中,∠BAC=90°,AB=AC,D为BC中点,且AE=CF.求证:△AED≌△CFD.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 建立坐标系,是为了定量地描述物体的位置及位置的变化 | |
| B. | 在建立坐标系时只需要确定正方向即可,与规定的正方向同向为正,与规定的正方向反向则为负 | |
| C. | 只能在水平方向建立直线坐标系 | |
| D. | 建立好直线坐标系后,可以用(x,y)表示物体的位置 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 捐 款 (元) | 5 | 10 | 20 | A | 30 |
| 人 数 | 18 | 20 | B | 4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
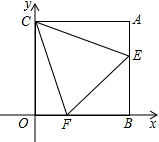 如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.
如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com