
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
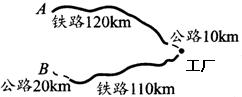 如图所示,某工厂与A、B两地由公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地销售,公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15000元,铁路运费97200元.
如图所示,某工厂与A、B两地由公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地销售,公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15000元,铁路运费97200元.查看答案和解析>>
科目:初中数学 来源: 题型:
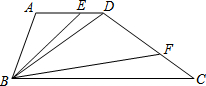 如图,在梯形ABCD中,AD∥BC,AD=AB,∠ABC=2∠C,E与F分别为边AD与DC上的两点,且有∠EBF=∠C.
如图,在梯形ABCD中,AD∥BC,AD=AB,∠ABC=2∠C,E与F分别为边AD与DC上的两点,且有∠EBF=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:
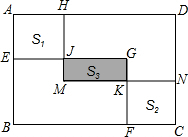 如图,在矩形ABCD中,矩形EBFG通过平移变换得到矩形HMND,点E、F、N、H都在矩形ABCD的边上.若BE=3,BF=4,4S3=S1+S2,且四边形AEJH和CFKN都是正方形,则图中空白部分的面积为
如图,在矩形ABCD中,矩形EBFG通过平移变换得到矩形HMND,点E、F、N、H都在矩形ABCD的边上.若BE=3,BF=4,4S3=S1+S2,且四边形AEJH和CFKN都是正方形,则图中空白部分的面积为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com