
【题目】任何一个正整数![]() 都可以写成两个正整数相乘的形式,我们把两个乘数的差的绝对值最小的一种分解
都可以写成两个正整数相乘的形式,我们把两个乘数的差的绝对值最小的一种分解![]() 称为正整数
称为正整数![]() 的最佳分解,并定义一个新运算
的最佳分解,并定义一个新运算![]() .例如:12=1×12=2×6=3×4,则
.例如:12=1×12=2×6=3×4,则![]() .那么以下结论中:①F(2)=
.那么以下结论中:①F(2)=![]() ;②F(24)=
;②F(24)=![]() ;③若
;③若![]() 是一个完全平方效,则
是一个完全平方效,则![]() ;④若
;④若![]() 是一个完全立方数(即
是一个完全立方数(即![]() ,
,![]() 是正整数),则
是正整数),则![]() .正确的个数为( )
.正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人用4张扑克牌(分别是红桃2,红桃3,黑桃4,方片5)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先取一张,取出的牌不放回,乙从剩余的牌中取一张.
(1)设![]() 、
、![]() 分别表示甲、乙取出的牌面上的数字,写出
分别表示甲、乙取出的牌面上的数字,写出![]() 的所有结果;
的所有结果;
(2)若甲取到红桃3,则乙取出的牌面数字比3大的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 是
是![]() 轴上一动点,要使点
轴上一动点,要使点![]() 关于直线
关于直线![]() 的对称点刚好落在
的对称点刚好落在![]() 轴上,则此时点
轴上,则此时点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A,B,O,C为数轴上四点,点A对应数![]() ,点O对应0,点C对应3,
,点O对应0,点C对应3,![]() (AB表示点A到点B的距离).
(AB表示点A到点B的距离).

(1)填空:点C到原点O的距离______,点B对应的数______.(用含有a的式子)
(2)如图2,将一刻度尺放在数轴上,刻度尺上“6cm”和“8.7cm”分别对应数轴上的点O和点C,若![]() ,求a的值和点A在刻度尺上对应的刻度。
,求a的值和点A在刻度尺上对应的刻度。
(3)如图3,在(2)的条件下,点A以1单位长度/秒的速度向右运动,同时点C向左运动,若运动3秒时,点A和点C到原点O的距离相等,求点C的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB:y=kx+4(k≠0)与x轴,y轴,交于A、B两点,点C是BO的中点且tan∠ABO=![]()
(1)求直线AC的解析式;
(2)若点M是直线AC的一点,当![]() 时,求点M的坐标.
时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
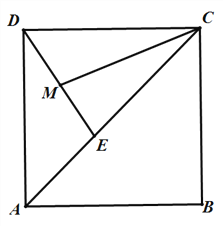
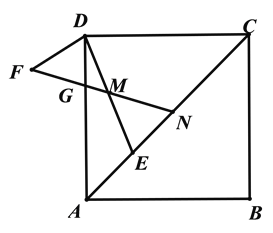
【题目】在菱形ABCD中,AC是对角线,CD=CE,连接DE,点M是线段DE的中点.
(1)如图1,连接CM,若AC=16,CD=10,求DE的长
(2)如图2,点F在菱形的外部,DF=DM,且∠CDA=∠FDE,连接FM交AD于点G,FM的延长线交AC于点N,求证:CN=AG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数![]() ,如果
,如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为![]() .例如
.例如![]() ,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以
,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以![]() .
.
(1)计算:![]() 和
和![]() ;
;
(2)若![]() 是“相异数”,证明:
是“相异数”,证明:![]() 等于
等于![]() 的各数位上的数字之和.
的各数位上的数字之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
(1)求证:△BCE≌△DCF;
(2)OG与BF有什么数量关系?证明你的结论;
(3)若GE·GB=4-2![]() ,求正方形ABCD的面积.
,求正方形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com