
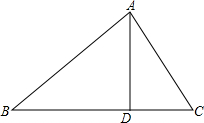
 有一块三角形铁皮ABC,已知最长边BC=12,高AD=8,要把它加工成一个矩形铁皮,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,问:加工成的矩形铁皮的面积最大值是多少平方厘米?
有一块三角形铁皮ABC,已知最长边BC=12,高AD=8,要把它加工成一个矩形铁皮,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,问:加工成的矩形铁皮的面积最大值是多少平方厘米? 分析 如图,矩形EFGH的顶点E在AB上,H点在AC上,FG在BC上,EH交AD于M,设EF=x,则MD=x,先证明△AEH∽△ABC,利用相似比可表示出EH=$\frac{3}{2}$(8-x),则利用矩形面积公式得到S矩形EFGH=x•$\frac{3}{2}$(8-x),然后利用二次函数的性质求S的最大值即可.
解答 解: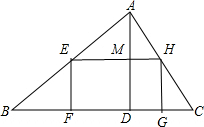 如图,矩形EFGH的顶点E在AB上,H点在AC上,FG在BC上,EH交AD于M,
如图,矩形EFGH的顶点E在AB上,H点在AC上,FG在BC上,EH交AD于M,
设EF=x,则MD=x,
∵EH∥BC,
∴△AEH∽△ABC,
∴$\frac{EH}{BC}$=$\frac{AM}{AD}$,即$\frac{EH}{12}$=$\frac{8-x}{8}$,
∴EH=$\frac{3}{2}$(8-x),
∴S矩形EFGH=x•$\frac{3}{2}$(8-x)=-$\frac{3}{2}$x2+12x=-$\frac{3}{2}$(x-4)2+24,
∵a=-$\frac{3}{2}$,
∴当x=4时,S矩形EFGH有最大值,最大值为24.
答:加工成的矩形铁皮的面积最大值是24平方厘米.
点评 本题考查了相似三角形的应用:通过构建三角形相似,利用相似三角形的性质即相似三角形的对应边的比相等进行几何计算.也考查了二次函数的性质.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | 不相交的两条直线是平行线 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 从直线外一点作这条直线的垂线段叫点到这条直线的距离 | |
| D. | 互余且相等的两角都是45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
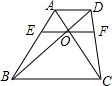 如图,在梯形ABCD中,AD∥BC,AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E、F.下列各式中不正确的是( )
如图,在梯形ABCD中,AD∥BC,AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E、F.下列各式中不正确的是( )| A. | $\frac{AE}{EB}$=$\frac{DF}{FC}$ | B. | $\frac{OA}{OC}$=$\frac{OD}{OB}$ | C. | $\frac{AE}{AB}$=$\frac{DO}{BO}$ | D. | $\frac{CD}{CF}$=$\frac{BD}{BO}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
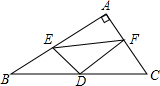 在Rt△ABC中,∠A=90°,点D为BC的中点,点E,F分别为AB,AC上的点,且ED⊥FD,以线段BE,EF,FC为边能否构成一个三角形?若能,请判断三角形的形状?
在Rt△ABC中,∠A=90°,点D为BC的中点,点E,F分别为AB,AC上的点,且ED⊥FD,以线段BE,EF,FC为边能否构成一个三角形?若能,请判断三角形的形状?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com