
【题目】如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE= . 
【答案】12或5
【解析】解:作AF⊥CE于F,DM⊥AF于M,如图所示:
则四边形DEFM是矩形,AF=17,∠AMD=90°,
∴∠EDM=90°,
∵四边形ABCD是正方形,
∴AD=CD=13,∠ADC=∠EDM=90°,
∴∠ADM=∠CDE,
在△ADM和△CDE中, 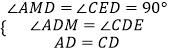 ,
,
∴△ADM≌△CDE(AAS),
∴DM=DE,AM=CE,
∴四边形DEFM是正方形,
∴DM=FM,
设AM=CE=x,则DM=FM=17﹣x,
在Rt△ADM中,由勾股定理得:x2+(17﹣x)2=132,
解得:x=12或x=5,
∴CE=12,或CE=5;
故答案为:12或5.
作AF⊥CE于F,DM⊥AF于M,由AAS证明△ADM≌△CDE,得出DM=DE,AM=CE,证出四边形DEFM是正方形,得出DM=FM,设AM=CE=x,则DM=FM=17﹣x,在Rt△ADM中,由勾股定理得出方程,解方程即可.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+
x2+ ![]() x﹣2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴.
x﹣2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴. 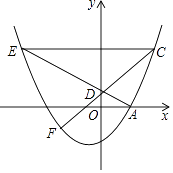
(1)求m,n的值;
(2)连结CD并延长交抛物线于点F,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC.AD的中点,AF∥BC交CE的延长线于F.则四边形AFBD的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线C1:y=a(x- ![]() )2+h分别与x轴、y轴交于点A(1,0)和点B(0,-2),将线段AB绕点A逆时针旋转90°至AP.
)2+h分别与x轴、y轴交于点A(1,0)和点B(0,-2),将线段AB绕点A逆时针旋转90°至AP.
(1)求点P的坐标及抛物线C1的解析式;
(2)将抛物线C1先向左平移2个单位,再向上平移1个单位得到抛物线C2 , 请你判断点P是否在抛物线C2上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校餐厅计划购买12张餐桌和若干把餐椅,先从甲、乙两个商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为60元,甲商场规定:购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌、餐椅均按报价的八折销售.
(1)若学校计划购买12张餐桌和12把餐椅,则到甲商场购买所需的费用为 ;到乙商场购买所需的费用为
(2)若学校计划购买![]()
![]() 把餐椅,则到甲商场购买所需的费用为 ;到乙商场购买所需的费用为 ;
把餐椅,则到甲商场购买所需的费用为 ;到乙商场购买所需的费用为 ;
(3)若学校计划购进20张餐桌和40把餐椅,请通过计算说明,到哪个商场购买合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t >0)秒.
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒1个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问点P运动多少秒时P、Q两点相遇?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出相应图形,并求出线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个多位正整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”.例如:49与76,因为4+9=7+6=13,所以49与76互为“调和数”;又如:225与18,因为2+2+5=1+8=9,所以225与18互为“调和数”.
(1)362与________互为“调和数”(写出一个即可);
(2)若两位数![]() 与75是一对“调和数”,且
与75是一对“调和数”,且![]() 的十位数字是个位数字的2倍,求
的十位数字是个位数字的2倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com