Question

16．等腰三角形一腰上的高与另一腰的夹角为30°，腰长为2cm，则其面积为$\sqrt{3}$cm²．

Answer 1

分析 本题要分情况讨论．当等腰三角形的顶角是钝角或者等腰三角形的顶角是锐角两种情况，在等腰三角形腰上的高与另一腰构建的直角三角形中，已知了30°的特殊角，通过解直角三角形即可求出高的长度，进而求出面积．

解答 解：①当为锐角三角形时，如图1，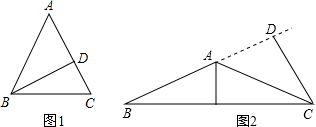
在Rt△ABD中，∠ABD=30°，AB=2cm，
BD=AB•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$（cm），
所以三角形的面积为$\frac{1}{2}$×2cm×$\sqrt{3}$cm=$\sqrt{3}$cm²，
②当为钝角三角形时，如图2，
在Rt△ACD中，∠ACD=30°，AC=2cm，
CD=AC•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$（cm），
所以三角形的面积为$\frac{1}{2}$×2cm×$\sqrt{3}$cm=$\sqrt{3}$cm²，
故答案为：$\sqrt{3}$．

点评 本题主要考查了等腰三角形的性质以及解直角三角形的应用．准确画出图形利用数形结合是解题的关键．