
| A. | 正三角形和正四边形 | B. | 正三角形和正六边形 | ||
| C. | 正四边形和正八边形 | D. | 正四边形和正十二边形 |
分析 分别求出各个正多边形每个内角的度数,再结合镶嵌的条件即可作出判断.
解答 解:正三角形的每个内角60°,正四边形的每个内角是90°,正六边形的每个内角是120°,正八边形的每个内角为180°-360°÷8=135°;正十二边形每个内角是180°-360°÷12=150°.
A、3×60°+2×90°=360°,即3个正三角形和2个正四边形可以密铺,故本选项错误;
B、2×60°+2×120°=360°,即2个正三角形和2个正六边形可以密铺,故本选项错误;
C、90°+2×135°=360°,即1个正四边形和2个正八边形可以密铺,故本选项错误;
D、设m个正四边形和n个正十二边形可以密铺,则90m+150n=360°,即m=4-2n+$\frac{1}{3}$n,那么n为3的倍数,显然n取任何3的倍数的正整数时,m不能得正整数,故不能铺满,不可以密铺,故本选项正确.
故选D.
点评 本题考查了两个正多边形平整镶嵌的条件:这两个正多边形的内角的整数倍的和为360°,同时也考查了正多边形内角的计算方法.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
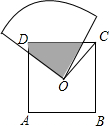 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )| A. | $\frac{1}{3}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{1}{2}$a2 | D. | $\frac{1}{4}$a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
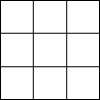 根据教材中所给的填幻方,请你找找规律,利用发现的规律将3,5,-7,1,7,-3,9,-5,-1这九个数字分别填入图中的九个方格中,使得横、竖、斜对角的所有三个数的和相等,则填入中央一格的数是( )
根据教材中所给的填幻方,请你找找规律,利用发现的规律将3,5,-7,1,7,-3,9,-5,-1这九个数字分别填入图中的九个方格中,使得横、竖、斜对角的所有三个数的和相等,则填入中央一格的数是( )| A. | 1 | B. | -1 | C. | 3 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
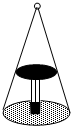 如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )
如图,圆桌正上方的一灯泡发出的光线照射到桌面后在地面上形成(圆形)的示意图.已知桌面半径为0.6米,桌面离地面1米.若灯泡离地面3米,则地面上阴影部分的面积为( )| A. | 0.36π米2 | B. | 0.81π米2 | C. | 2π米2 | D. | 3.24π米2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com