
分析 根据矩形的性质求出∠B=∠C=90°,AB=CD=4,求出∠1=∠3,证△ABP∽△PCD,得出比例式,求出BP,解直角三角形求出即可.
解答 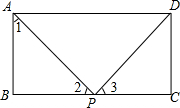
解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD=4,
∵∠APD=90°,
∴∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∴△ABP∽△PCD,
∴$\frac{AB}{CP}$=$\frac{BP}{CD}$,
∴$\frac{4}{10-BP}$=$\frac{BP}{4}$,
解得:BP=2或8,
∵tan∠APB=$\frac{AB}{BP}$,
∴∠APB的正切值为2或$\frac{1}{2}$.
故答案为:2或$\frac{1}{2}$.
点评 本题考查了解直角三角形,相似三角形的性质和判定,矩形的性质的应用,能求出BP的长是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
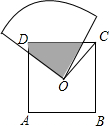 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )| A. | $\frac{1}{3}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{1}{2}$a2 | D. | $\frac{1}{4}$a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
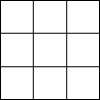 根据教材中所给的填幻方,请你找找规律,利用发现的规律将3,5,-7,1,7,-3,9,-5,-1这九个数字分别填入图中的九个方格中,使得横、竖、斜对角的所有三个数的和相等,则填入中央一格的数是( )
根据教材中所给的填幻方,请你找找规律,利用发现的规律将3,5,-7,1,7,-3,9,-5,-1这九个数字分别填入图中的九个方格中,使得横、竖、斜对角的所有三个数的和相等,则填入中央一格的数是( )| A. | 1 | B. | -1 | C. | 3 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com