练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．把（x-1）6展开得a6x6+a5x5+…+a2x2+a1x+a0，求a0+a2+a4+a6的值．

    分析 将x=1代入代数式得a6x6+a5x5+…+a2x2+a1x+a0=a6+a5+…+a2+a1+a0=0，将x=-1代入得：a6x6+a5x5+…+a2x2+a1x+a0=a6-a5+…+a2-a1+a0=64，最后将两式相加，从而可求得a0+a2+a4+a6的值．

    解答 解：将x=1代入得：（x-1）6=（1-1）6=0，即a6+a5+…+a2+a1+a0=0①，
    将x=-1代入得：：（x-1）6=（-1-1）6=64，即a6-a5+a4-a3+a2-a1+a0=64②，
    ①+②得：2（a0+a2+a4+a6）=64，
    ∴a0+a2+a4+a6=32．

    点评 本题主要考查得是代数式的求值问题，将x=1，x=-1代入求得a6+a5+…+a2+a1+a0=0和a6-a5+a4-a3+a2-a1+a0=64是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

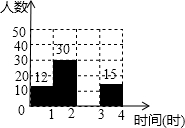    5．阅读对人的影响是巨大的，一本好书往往能改变一个人的一生．某校为了解全校1800名学生双休日的阅读时间，学校随机调查了七、八、九年级部分同学，并用得到的数据绘制成不完整的统计图表如图所示：
    阅读时间频数（人数）频率
    0～1120.12
    1～2300.3
    2～3x0.4
    3～418y
    合计m1
    （1）x=40，y=0.18；
    （2）请将频数分布直方图补充完整；
    （3）根据调查数据估计，该校同学双休日阅读时间在2小时以上的学生的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

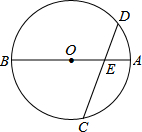    6．如图，AB为⊙O的直径，弦CD与AB相交于点E，且OE=DE，试确定$\widehat{BC}$与$\widehat{AD}$之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．在（-2），（-2）3，|-2|，（-2）2，-22中，负数有（　　）个．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解方程：$\frac{1}{2}${$\frac{1}{2}$[$\frac{1}{2}$（$\frac{1}{2}y$-3）-3]-3}=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．两个矩形如图1摆放在直线MN上，AD=EH=1，CD=DE=EF=2，将矩形ABCD绕点D顺时针旋转角α，同时将矩形EFGH绕点E逆时针旋转角α，其中0°＜α＜90°．
    （1）如图2，当点C和F重合时，α=30°；
    （2）如图3，当两个矩形的重叠部分为正方形时，α=45°，重叠部分的面积S=6-4$\sqrt{2}$；
    （3）如图4，当旋转到点B与点G重合时，设DC与EF交于P，BP的延长线交DE于Q，线段BQ与DE的关系是垂直平分相等，利用你的结论（不用证明），计算两个矩形重叠部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释，例如：图A可以用来解释a2+2ab+b2=（a+b）2，实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解．

    （1）图B可以解释的代数恒等式是2a2+2ab=2a（a+b）．
    （2）现有足够多的正方形和矩形卡片（如图C），试在下面的虚线方框中画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形（每两张纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使该矩形的面积为a2+ab-2b2，并利用你所画的图形面积对a2+ab-2b2进行因式分解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．（1）探究：如图1和2，四边形ABCD中，已知AB=AD，∠BAD=90°，点E、F分别在BC、CD上，∠EAF=45°．
    ①如图1，若∠B、∠ADC都是直角，把△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，则能证得EF=BE+DF，请写出推理过程；
    ②如图2，若∠B、∠D都不是直角，则当∠B与∠D满足数量关系∠B+∠D=180°时，仍有EF=BE+DF；
    （2）拓展：如图3，在△ABC中，∠BAC=90°，AB=AC=2$\sqrt{2}$，点D、E均在边BC上，且∠DAE=45°．若BD=1，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

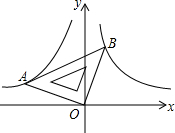    6．如图，一块等腰直角三角板AOB的直角顶点O与坐标原点生命，点B、A分别在第一、二象限，反比例函数y=$\frac{{k}_{1}}{x}$、y=$\frac{{k}_{2}}{x}$的图象分别经过点A、B，若点A的坐标是（-3，1），分别求出k1，k2的值．

    查看答案和解析>>

    同步练习册答案