
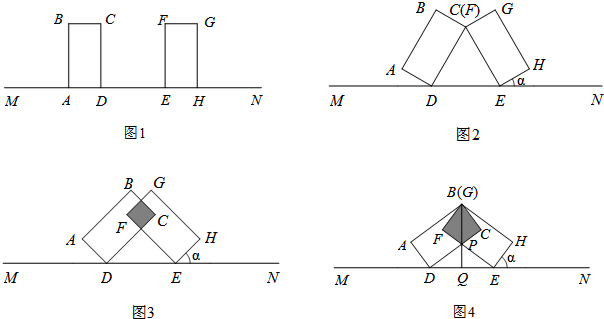
分析 (1)由CD=FE=DE=2,得到△CDE为等边三角形,则∠DCE=60°,得到∠1=180°-∠ADC-∠CDE=180°-90°-60°=30°,得到α=30°;
(2)由四边形MFNC为正方形,而矩形ABCD绕点D顺时针旋转和矩形EFGH绕点E逆时针旋转相同的角度.得到NF=NC,∠FNC=90°,则∠DNE=90°,ND=NE,得到∠NDE=∠NED=45°,所以∠1=180°-90°-45°=45°,即α=45°,由于△DFE是等腰直角三角形,DE=2,可求出DF=$\sqrt{2}$,CF=2-$\sqrt{2}$,即可求出重合正方形面积;
(3)垂直平分相等,可证明△BFP≌△EQP,得到PF=QE,在△BFP中用勾股定理列方程求出PF,即可求出重合部分面积.
解答 解:(1)如图2,
∵CD=FE=DE=2,
∴△CDE为等边三角形,
∴∠DCE=60°,
∴∠MDA=180°-∠ADC-∠CDE=180°-90°-60°=30°,
而∠MDA等于旋转角,
∴α=30°;
(2)如图3,∵四边形MFNC为正方形,
而矩形ABCD绕点D顺时针旋转和矩形EFGH绕点E逆时针旋转相同的角度.
∴NF=NC,∠FNC=90°,
∴∠DNE=90°,ND=NE,
∴∠NDE=∠NED=45°,
∴∠ADM=180°-90°-45°=45°,
∴α=45°.
∵△DEF是等腰直角三角形,DE=2,
∴DF=$\sqrt{2}$,CF=2-$\sqrt{2}$,
∴S正方形=(2-$\sqrt{2}$)2=6-4$\sqrt{2}$;
(3)线段BQ与DE的关系是:垂直平分相等.
如图4,
在△BFP和△EQP中
$\left\{\begin{array}{l}{∠F=∠EQP=90°}\\{∠BPF=∠EPQ}\\{BF=QE=1}\end{array}\right.$
∴△BFP≌△EQP,
∴PQ=PF,
设PF=x,则BP=2-x,
∵BP2=PF2+BF2,
∴(2-x)2=12+x2
∴x=$\frac{3}{4}$,
∴S四边形BFPC=2S△BFP=2×$\frac{1}{2}$×1×$\frac{3}{4}$=$\frac{3}{4}$.
故答案为:(1)30°;(2)45°,$6-4\sqrt{2}$;(3)垂直平分相等.
点评 本题考查了旋转的性质、矩形的性质、等边三角形的判定与性质、正方形的判定与性质、全等三角形的判定与性质、以及勾股定理和图形面积计算等知识,熟练运用旋转的性质以及具有较强的逻辑推理能力是解决问题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
 小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与他时间的变化情况,如图所示.
小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与他时间的变化情况,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
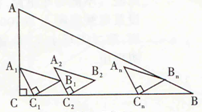 如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )
如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )| A. | $\frac{1}{7}$ | B. | $\frac{\sqrt{5}}{7}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{8\sqrt{5}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com