
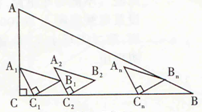
 ��ͼ���ڡ�ABC�У���C=90�㣬AC=2��BC=4����A1B1C1����A2B2C2����A3B3C3��������AnBnCn��n����ͬ�ĵ���ֱ�������Σ���ֱ�Ƕ���C1��C2��C3������Cn����CB���ϣ���A1��AC�ϣ�A2C2������B1��ƽ����A1C1��A3C3������B2��ƽ����A2C2������AnCn����Bn-1��ƽ����An-1Cn-1����A1C=2CC1����n=7ʱ����B7��������AB�ߣ������С�ĵ���ֱ�������ε�ֱ�DZ߳�Ϊ��������
��ͼ���ڡ�ABC�У���C=90�㣬AC=2��BC=4����A1B1C1����A2B2C2����A3B3C3��������AnBnCn��n����ͬ�ĵ���ֱ�������Σ���ֱ�Ƕ���C1��C2��C3������Cn����CB���ϣ���A1��AC�ϣ�A2C2������B1��ƽ����A1C1��A3C3������B2��ƽ����A2C2������AnCn����Bn-1��ƽ����An-1Cn-1����A1C=2CC1����n=7ʱ����B7��������AB�ߣ������С�ĵ���ֱ�������ε�ֱ�DZ߳�Ϊ��������| A�� | $\frac{1}{7}$ | B�� | $\frac{\sqrt{5}}{7}$ | C�� | $\frac{\sqrt{5}}{5}$ | D�� | $\frac{8\sqrt{5}}{5}$ |
���� ����B1D��BC��D��������CC1=x��Ȼ���ʾ��A1C=2x��A1C1=$\sqrt{5}$x�������֪�߶����������Ӧ�ߵı�����Ҽн����֤�á�ABC�ס�C1CA1���������������ε����ʵõ���CA1C1=��B���Ӷ�֤��C1CA1�ա�B1C1D��Ȼ�����CC1+C1B=BC�г�����x+4x=4�����xֵ���ɵõ�a1=A1C1=$\sqrt{5}$x=$\frac{4\sqrt{5}}{5}$��
����B2D��BC��D����ڣ�1�������Ƶõ�C1CA1�ס�C2C1B1���������������εĶ�Ӧ�ߵı���ȵõ�C1C2=$\frac{5}{2}$x���Ӷ�����CC1+C1C2+C2D=BC�õ�����x+$\frac{5}{2}$x+4x=4���x=$\frac{8}{15}$�ɵõ�a2=A1C1=$\sqrt{5}$x=$\frac{8\sqrt{5}}{15}$��
����BnD��BC��D���ɵڣ�1������2����С���֪BCn=4x���Ӷ��õ�C1C2=C2C3=��=Cn-1Cn=$\frac{5}{2}$x������CC1+C1C2+C2C3+��+CnD=BC�õ�����x+$\frac{5}{2}$x��n-1��+4x=4���x=$\frac{8}{5n+5}$�ɵõ�an=A1C1=$\sqrt{5}$x=$\frac{8\sqrt{5}}{5n+5}$��
��� 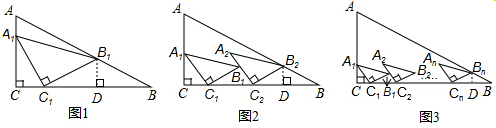 �⣺����ͼ1����B1D��BC��D��
�⣺����ͼ1����B1D��BC��D��
��CC1=x����A1C=2x��A1C1=$\sqrt{5}$x��
��AC=2��BC=4��
��$\frac{AC}{BC}$=$\frac{C{C}_{1}}{{A}_{1}C}$
�ߡ�ACB=��C1CA1=90�㣬
���ABC�ס�C1A1C��
���CA1C1=��B��
�ߡ�CA1C1=90��-��A1C1C=��B1C1D��
��C=��B1DC1=90�㣬A1C1=C1B1��
���C1CA1�ա�B1DC1��
��C1D=A1C=2x����CA1C1=��B1C1D=��B��
��BD=C1D=2x��BC1=4x��
��CC1+C1B=BC��
��x+4x=4��
��ã�x=$\frac{4}{5}$��
��a1=A1C1=$\sqrt{5}$x=$\frac{4\sqrt{5}}{5}$��
����ͼ2����B2D��BC��D��
��CC1=x����A1C=2x��A1C1=B1C1=A2C2=B2C2=$\sqrt{5}$x��
�ɢٿ�֪BC2=C2D+BD=4x��
��A1C1��A2C2��
���A1C1C=��B1C2C1��
�ߡ�C=��C1B1C2=90�㣬
���C1CA1�ס�C2B1C1��
��$\frac{{C}_{1}{B}_{1}}{{C}_{1}{C}_{2}}$=$\frac{{A}_{1}C}{{A}_{1}{C}_{1}}$��
��C1C2=$\frac{5}{2}$x��
��CC1+C1C2+BC2=BC��
��x+$\frac{5}{2}$x+4x=4��
��x=$\frac{8}{15}$��
��a2=A1C1=$\sqrt{5}$x=$\frac{8\sqrt{5}}{15}$��
����ͼ3����BnD��BC��D��
�ɢ٢ڿ�֪BCn=4x��
C1C2=C2C3=��=Cn-1Cn=$\frac{5}{2}$x��
��CC1+C1C2+C2C3+��+BCn=BC��
��x+$\frac{5}{2}$x��n-1��+4x=4��
��x=$\frac{8}{5n+5}$��
��an=A1C1=$\sqrt{5}$x=$\frac{8\sqrt{5}}{5n+5}$��
��a7=$\frac{8\sqrt{5}}{5��7+5}$=$\frac{\sqrt{5}}{5}$��
��ѡC��
���� ���⿼�������������ε��ж������ʣ�����ֱ�������ε����ʣ����ɶ�������ȷ�������������ǽ���Ĺؼ���


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
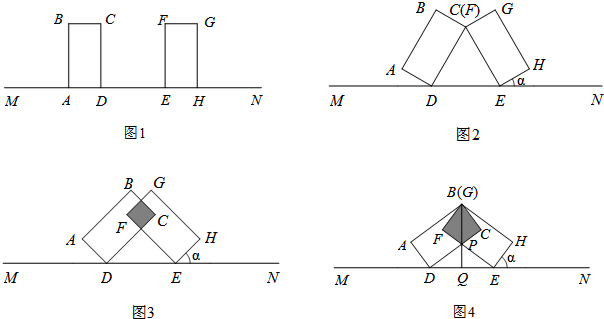
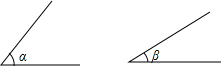 ��ͼ��ʾ����֪�Ϧ����Ϧ£��ҡϦ����Ϧ¾�Ϊ��ǣ����AOB��ʹ�����ڡϦ���Ϧµĺͣ�
��ͼ��ʾ����֪�Ϧ����Ϧ£��ҡϦ����Ϧ¾�Ϊ��ǣ����AOB��ʹ�����ڡϦ���Ϧµĺͣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
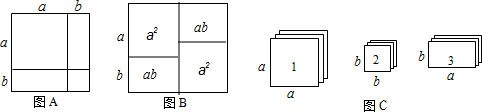
 ��ͼ����Ҫ��һ�������μ�����������һ�߿�ǽ��ǽ������һ��2�����ţ��������������Χ�ɣ�����ܳ�33�ף�Χ�ɳ����εļ�������֮�����ܲ����п�϶����
��ͼ����Ҫ��һ�������μ�����������һ�߿�ǽ��ǽ������һ��2�����ţ��������������Χ�ɣ�����ܳ�33�ף�Χ�ɳ����εļ�������֮�����ܲ����п�϶�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com