
 小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与他时间的变化情况,如图所示.
小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与他时间的变化情况,如图所示.分析 (1)根据图象可得图象表示离家距离与时间之间的关系,时间是自变量,离家距离是因变量;
(2)根据图象可得10时和11时,他分别离家15千米、20千米;
(3)根据图象可得他到达离家最远的地方是13时,离家30千米;
(4)根据图象可得11时到13时他行驶的距离;
(5)利用待定系数法解答解析式即可.
解答 解:(1)图象表示离家距离与时间之间的关系,时间是自变量,离家距离是因变量;
(2)10时和11时,他分别离家15千米、20千米;
(3)他到达离家最远的地方是13时,离家30千米;
(4)11时到13时他行驶了30-20=10千米;
(5)设离家距离为S,时间为t,其解析式为S=kt+b,
可得:$\left\{\begin{array}{l}{14k+b=30}\\{17k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-10}\\{b=170}\end{array}\right.$,
所以解析式为:S=-10t+170.
点评 此题考查函数图象问题,关键是根据图象得出信息和利用待定系数法解解析式的应用.


科目:初中数学 来源: 题型:选择题
| A. | m<3 | B. | m>3 | C. | m<0 | D. | m>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
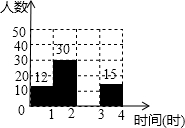 阅读对人的影响是巨大的,一本好书往往能改变一个人的一生.某校为了解全校1800名学生双休日的阅读时间,学校随机调查了七、八、九年级部分同学,并用得到的数据绘制成不完整的统计图表如图所示:
阅读对人的影响是巨大的,一本好书往往能改变一个人的一生.某校为了解全校1800名学生双休日的阅读时间,学校随机调查了七、八、九年级部分同学,并用得到的数据绘制成不完整的统计图表如图所示:| 阅读时间 | 频数(人数) | 频率 |
| 0~1 | 12 | 0.12 |
| 1~2 | 30 | 0.3 |
| 2~3 | x | 0.4 |
| 3~4 | 18 | y |
| 合计 | m | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com