
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-![]() x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
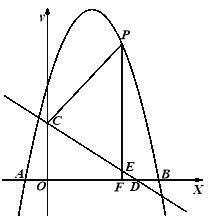
(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。
【答案】(1)、y=-![]() +4x+5;(2)、m=2或m=
+4x+5;(2)、m=2或m=![]() ;(3)、
;(3)、![]() ,
,![]() (4,5),
(4,5),![]() .
.
【解析】
试题分析:(1)、利用待定系数法进行求解;(2)、首先设出点P、点E和点F的坐标,求出PE的长度,然后根据点E在点F的上方和下方两种情况分别进行计算;(3)、根据△CME和△COD相似来进行求解.
试题解析:(1)、将A、B两点的坐标代入得:![]() 解得:
解得:![]()
∴抛物线的解析式为:y=-![]() +4x+5
+4x+5
、设点P的坐标为(m,-![]() +4m+5),则E(m,-
+4m+5),则E(m,-![]() m+3),F(m,0)
m+3),F(m,0)
∵点P在x轴上方,要使PE=5EF,点P应在y轴右侧 ∴0<m<5
PE=-![]() +4m+5-(-
+4m+5-(-![]() m+3)=-
m+3)=-![]() +
+![]() m+2
m+2
①当点E在点F上方时,EF=-![]() m+3 ∵PE=5EF ∴-
m+3 ∵PE=5EF ∴-![]() +
+![]() m+2=5(-
m+2=5(-![]() m+3)
m+3)
解得:![]() =2,
=2,![]() (舍去)
(舍去)
②当点E在点F下方时,EF=![]() m-3 ∵PE=5EF ∴-
m-3 ∵PE=5EF ∴-![]() +
+![]() m+2=5(
m+2=5(![]() m-3)
m-3)
解得:![]() ,
,(舍去)
(3)、点P的坐标为![]() ,
,![]() (4,5),
(4,5),![]()


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=![]() (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆E是三角形ABC的外接圆, ∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.
(1)求三角形ABC的外接圆直径;
(2)求过ABC三点的抛物线的解析式;
(3)设P是(2)中抛物线上的一个动点,且三角形AOP为直角三角形,则这样的点P有几个?(只需写出个数,无需解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,作
,作![]() ,垂足为点
,垂足为点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() .
.

(1)如图中的图1,求证:![]() ;
;
(2)如图中的图2,![]() 是
是![]() 的中点,若
的中点,若![]() ,
,![]() ,在不添加任何辅助线的情况下,请找出图中的四个三角形,使得每个三角形的面积都等于
,在不添加任何辅助线的情况下,请找出图中的四个三角形,使得每个三角形的面积都等于![]() 面积的
面积的![]() 倍,并说明理由.
倍,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
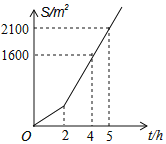
A. 200B. 300C. 400D. 500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受猪流感的影响,4月初某地猪肉价格大幅度下调,下调后每斤猪肉价格是原价格的![]() ,原来用60元买到的猪肉下调后可多买2斤.4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.
,原来用60元买到的猪肉下调后可多买2斤.4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.
(1)求4月初猪肉价格下调后每斤多少元?
(2)求5、6月份猪肉价格的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
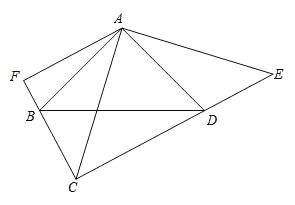
【题目】如图, BAD CAE 90 , AB AD , AE AC , ABD ADB ACE AEC 45 ,AF CF ,垂足为 F .
(1)若 AC 10 ,求四边形 ABCD 的面积;
(2)求证: CE 2 AF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
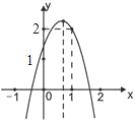
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△OAB是⊙O的内接三角形,∠AOB=120°,过O作OE⊥AB于点E,交⊙O于点C,延长OB至点D,使OB=BD,连CD.
(1)求证: CD是⊙O切线;
(2)若F为OE上一点,BF的延长线交⊙O于G,连OG,![]() ,CD=6
,CD=6![]() ,求S△GOB.
,求S△GOB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com