
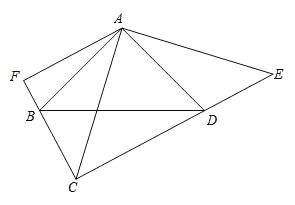
【题目】如图, BAD CAE 90 , AB AD , AE AC , ABD ADB ACE AEC 45 ,AF CF ,垂足为 F .
(1)若 AC 10 ,求四边形 ABCD 的面积;
(2)求证: CE 2 AF .
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案;
(2)过点A作AG⊥CG,垂足为点G,求出AF=AG,求出CG=AG=GE,即可解决问题.
(1)解:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD
∴∠BAC=∠EAD,
在△ABC和△ADE中,
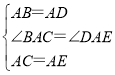 ,
,
∴△ABC≌△ADE(SAS),
∵S四边形ABCD=S△ABC+S△ACD,
∴S四边形ABCD=S△ADE+S△ACD=S△ACE=![]() ×102=50;
×102=50;
(2)证明:∵△ACE是等腰直角三角形,
∴∠ACE=∠AEC=45°,
由△ABC≌△ADE得:
∠ACB=∠AEC=45°,
∴∠ACB=∠ACE,
∴AC平分∠ECF;
过点A作AG⊥CG,垂足为点G,
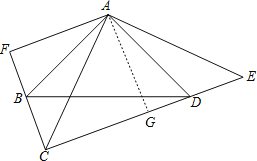
∵AC平分∠ECF,AF⊥CB,
∴AF=AG,
又∵AC=AE,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC=45°,
∴CG=AG=GE,
∴CE=2AG,
∴CE=2AF.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.
(1)求此二次函数的关系式;
(2)P为二次函数y=ax2+bx+c图象上一点,且S△ABP=S△ABC,求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线交于点O,点E是矩形外一点,![]() ,
,![]() ,
,![]() ,连接AE交BD于点F、连接CF.
,连接AE交BD于点F、连接CF.
![]() 求证:四边形BECO是菱形;
求证:四边形BECO是菱形;
![]() 填空:若
填空:若![]() ,则线段CF的长为______.
,则线段CF的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-![]() x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
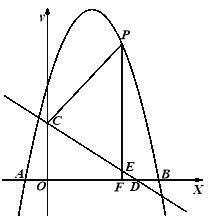
(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6cm,动点P从A点出发,在正方形的边上由A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示
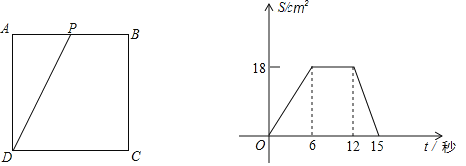
(1)求点P在BC上运动的时间范围;
(2)当t为何值时,△APD的面积为10cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-2x+4与x轴y轴相交于A,B两点,点C在线段AB上,且∠COA=45°.
(1)求点A,B的坐标;
(2)求△AOC的面积;
(3)直线OC上有一动点D,过点D作直线l(不与直线AB重合)与x,y轴分别交于点E,F,当△OEF与△ABO全等时,求直线EF的解析式.
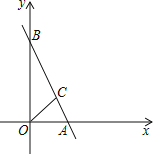
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级的体育老师为了了解本年级学生喜欢球类运动的情况,抽取了该年级部分学生对篮球、足球、排球、乒乓球的爱好情况进行了调查,并将调查结果绘制成如图两幅不完整的统计图(说明:每位学生只选一种自己最喜欢的一种球类),请根据这两幅图形解答下列问题:
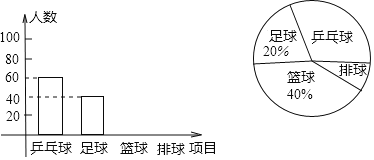
(1)在本次调查中,体育老师一共调查了多少名学生?
(2)将两个不完整的统计图补充完整;
(3)求出乒乓球在扇形中所占的圆心角的度数?
(4)已知该校有760名学生,请你根据调查结果估计爱好足球和排球的学生共计多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
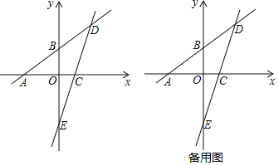
【题目】已知:如图,一次函数y=![]() x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为______;(直接写出结果)
(2)在x轴上求一点P使△PAD为等腰三角形,直接写出所有满足条件的点P的坐标.
(3)若点Q为线段DE上的一个动点,连接BQ.点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com