
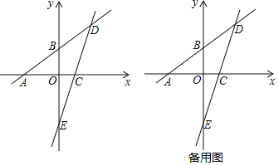
����Ŀ����֪����ͼ��һ�κ���y=![]() x+3��ͼ��ֱ���x�ᡢy���ཻ�ڵ�A��B�����뾭����C(2��0)��һ�κ���y=kx+b��ͼ���ཻ�ڵ�D����D�ĺ�����Ϊ4��ֱ��CD��y���ཻ�ڵ�E��
x+3��ͼ��ֱ���x�ᡢy���ཻ�ڵ�A��B�����뾭����C(2��0)��һ�κ���y=kx+b��ͼ���ཻ�ڵ�D����D�ĺ�����Ϊ4��ֱ��CD��y���ཻ�ڵ�E��
(1)ֱ��CD�ĺ�������ʽΪ______��(ֱ��д�����)
(2)��x������һ��Pʹ��PADΪ���������Σ�ֱ��д���������������ĵ�P�����꣮
(3)����QΪ�߶�DE�ϵ�һ�����㣬����BQ����Q�Ƿ����ij��λ�ã�����BQD����ֱ��BQ���ۣ�ʹ�õ�Dǡ������ֱ��AB�·���y���ϣ������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1)y=3x-6��(2)��P������Ϊ(![]() ��0)��(6��0)��(-14��0)��(12��0)��(3)���ڣ���Q������Ϊ(
��0)��(6��0)��(-14��0)��(12��0)��(3)���ڣ���Q������Ϊ(![]() ��
��![]() )
)
��������
(1)���D�����꣬������⣻
(2)��PA=PD����PA=AD��DP=AD����������ֱ���⼴�ɣ�
(3)����BD=BD����DQ=D��Q��������⣮
�⣺(1)����D�ĺ�����Ϊ4����һ�κ���y=![]() x+3����ʽ����ã�y=6������D������Ϊ(4��6)��
x+3����ʽ����ã�y=6������D������Ϊ(4��6)��
����C��D���������һ�κ�������ʽy=kx+b�ã�![]()
��ã� ![]()
�ʴ�Ϊ��y=3x-6��
(2)�ٵ�PA=PDʱ��
��B��AD���е㣬
�ʣ�����B�Ҵ�ֱ��AD��ֱ�߷���Ϊ��y=-![]() x+3��
x+3��
��y=0����x=![]() ��
��
����P������Ϊ(![]() ��0)��
��0)��
�ڵ�PA=ADʱ��
AD=![]() =10��
=10��
�ʵ�P������Ϊ(6��0)��(-14��0)��
�۵�DP=ADʱ��
ͬ���ɵã���P������Ϊ(12��0)��
�ʵ�P������Ϊ(![]() ��0)��(6��0)��(-14��0)��(12��0)��
��0)��(6��0)��(-14��0)��(12��0)��
(3)�跭ת���D����y���ϵĵ�ΪD�������Q������Ϊ(x��3x-6)��
��BD=BD����DQ=D��Q��
BD��=BD=![]() =5���ʵ�D��������Ϊ(0��-2)��
=5���ʵ�D��������Ϊ(0��-2)��
DQ2=D��Q2������x2+(3x-6+2)2=(x-4)2+(3x-6-6)2��
��ã�x=![]() ��
��
�ʵ�Q������Ϊ(![]() ��
��![]() )��
)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
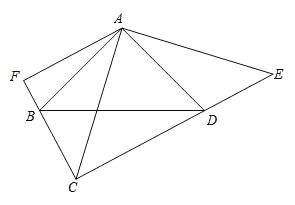
����Ŀ����ͼ�� BAD CAE 90 �� AB AD �� AE AC �� ABD ADB ACE AEC 45 ��AF CF ������Ϊ F .
��1���� AC 10 �����ı��� ABCD �������
��2����֤�� CE 2 AF .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
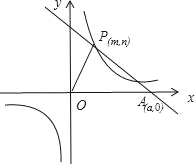
����Ŀ����֪��O������ԭ�㣬P��m��n����m��0���Ǻ���y=![]() ��k��0���ϵĵ㣬����P��ֱ��PA��OP��P��ֱ��PA��x��������ύ�ڵ�A��a��0����a��m��������OPA�����Ϊs����s=1+
��k��0���ϵĵ㣬����P��ֱ��PA��OP��P��ֱ��PA��x��������ύ�ڵ�A��a��0����a��m��������OPA�����Ϊs����s=1+![]() ��
��
��1����n=1ʱ�����A�����ꣻ
��2����OP=AP����k��ֵ��
��3����n��С��20����������k��![]() ����OP2����Сֵ��
����OP2����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����OAB����O���ڽ������Σ���AOB=120������O��OE��AB�ڵ�E������O�ڵ�C���ӳ�OB����D��ʹOB=BD����CD��
��1����֤�� CD����O���ߣ�
��2����FΪOE��һ�㣬BF���ӳ��߽���O��G����OG��![]() ��CD=6
��CD=6![]() ����S��GOB��
����S��GOB��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߶�AB��12cm����C���߶�AB�ϣ���D��E�ֱ���AC��BC���е㣮
��1������Cǡ����AB�е㣬��DE�ij���
��2����AC��4cm����DE�ij���
��3������CΪ�߶�AB�ϵ�һ�����㣨��C����A��B�غϣ�����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڽⷽ��![]() ʱ����������ķ�������
ʱ����������ķ�������![]() ������
������![]() �ɵ�
�ɵ�![]() ��������ʽ��ӿɵ�
��������ʽ��ӿɵ�![]() ����
����![]() ����ƽ���ɽ��
����ƽ���ɽ��![]() ����1��������
����1��������![]() ����1��ԭ���̵Ľ�.
����1��ԭ���̵Ľ�.
����ο�С���ķ����������з��̣�
(1)![]()
(2)![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
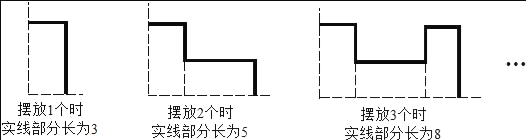
����Ŀ������ͬ�ľ��ο�Ƭ������ͼ��ʽ�ڷ���һ��ֱ���ϣ�ÿ�����ο�Ƭ��Ϊ2����Ϊ1���������ƣ��ڷ�2014��ʱ��ʵ�߲��ֳ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��AB��һ�㣬F��AD�ӳ�����һ�㣬��DF=BE��

��1����֤��CE=CF��
��2������G��AD�ϣ�����GCE=45������GE=BE+GD������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
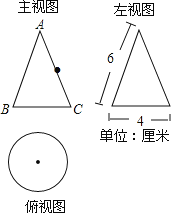
����Ŀ����ͼ��һ�������������ͼ��
��1��д���ü���������ƣ���������ʾ���ݼ������������ı������
��2�����һֻ����Ҫ������������еĵ�B�������ر�������AC���е�D��������������·�����·�̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com