
2011年3月10日12时58分,在云南盈江县发生5.8级地震,随后又相继发生里氏4.7级、里氏4.5级、里氏3.6级余震。灾情发生后,全国人民抗震救灾,众志成城。湖州市政府也筹集了抗震救灾物资共120吨准备运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
|
车型 |
甲 |
乙 |
丙 |
|
汽车运载量(吨/辆) |
5 |
8 |
10 |
|
汽车运费(元/辆) |
400 |
500 |
600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总车辆数为14辆,你能分别求出三种车型的车辆数吗?此时的运费又是多少元?
(1)甲种车型8辆,乙种车型10辆,(2)甲种车型2辆,乙种车型5辆,则丙种车型为7辆,7500元
【解析】
试题分析:(1)首先设需甲车x辆,乙车y辆,根据题意可得两个等量关系:①甲车x辆的运载量+乙车y辆的运载量=120吨,②甲车x辆的运费+乙车y辆的运费=8200元,根据等量关系列出方程,组成方程组,解方程组即可;
(2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆,根据运输物资的总量可得5a+8b+10(14-a-b)=120,再根据a、b、14-a-b均为正整数进行讨论计算出b=5,然后算出总运费即可.
(1)设需甲车x辆,乙车y辆,由题意得
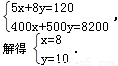
答:需甲种车型8辆,需乙种车型10辆;
(2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆.
由题意,得5a+8b+10(14-a-b)=120,
化简得5a+2b=20,解得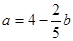
∵a、b、14-a-b均为正整数,
∴b只能等于5,从而a=2,14-a-b=7,
∴甲车需2辆,乙车需5辆,丙车需7辆,
共需运费400×2+500×5+600×7=7500(元),
答:三种车型的车辆数:甲车需2辆,乙车需5辆,丙车需7辆;共需运费7500元.
考点:二元一次方程和方程组的应用
点评:解题的关键是找出题目中的等量关系,根据运费和所运物资的总量列出方程求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
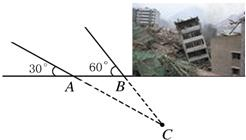 2011年3月10日,云南盈江县发生里氏5.8级地震.萧山金利浦地震救援队接到上级命令后立即赶赴震区进行救援.救援队利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3米,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果精确到0.1米,参考数据:
2011年3月10日,云南盈江县发生里氏5.8级地震.萧山金利浦地震救援队接到上级命令后立即赶赴震区进行救援.救援队利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3米,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果精确到0.1米,参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com