Question

8．已知直线y₁=2x+1与抛物线y₂=ax²+bx+c，抛物线y₂与y轴交于点A（0，5），与x轴分别交于B（1，0），C（5，0）两点．
（1）求抛物线的解析式并在同一坐标系中画出直线和抛物线的示意图；
（2）结合图象回答：
①y₂≥0时，x的取值范围；
②0＜x＜5时，y₂的取值范围；
③y₂≥y₁时，x的取值范围；
④关x于的方程ax²+bx+c=k有两个不等实根，k的取值范围是什么？
（3）将抛物线在x轴下方部分沿x轴翻折到轴上方后，B，C间的部分向左平移n（n＞2）个单位后得到的图象记为图象G，同时将y₁向上平移n个单位，请结合图象回答：当平移后的直线与图象有公共点时，求n的取值范围．

Answer 1

分析 （1）根据待定系数法即可求解．
（2）①y₂≥0时，图象在x轴上方即可写出y₂的范围．
②0＜x＜5时，在图象上可以直接得出y₂的范围．
③解方程组求出交点坐标，然后写出x的取值范围．
④由图象直接可知结论．
（3）翻折后的B、C之间抛物线为y=-（x²-6x+5）=-X²+6X-5=-（x-1）（x-5），（1≤x≤5），平移后的抛物线：y=-（x-1+n）（x-5+n），1-n＜x＜5-n，此时直线平移后的解析式为y=2x+1+n，如果平移后的直线与平移后的二次函数相切，则方程2x+1+n=-（x-1+n）（x-5+n）有两个相等的实数根，即x²-（4-2n）x+n²-5n+6=0有两个相等的实数根，△=16-16n+4n²-4n²+20n-24=0即n=2求出的n的值与已知n＞0相矛盾，得出平移后的直线与抛物线有两个公共点，设两个临界的交点为（1-n，0），（5-n，0），代入直线的解析式，求出n的值，即可得出答案．

解答 解：（1）由题意$\left\{\begin{array}{l}{c=5}\\{a+b+c=0}\\{25a+5b+c=0}\end{array}\right.$，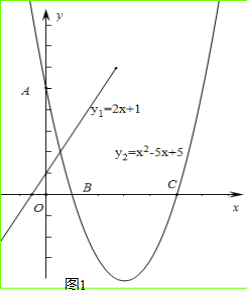
解得$\left\{\begin{array}{l}{a=1}\\{b=-6}\\{c=5}\end{array}\right.$，．
故抛物线的解析式为y=x²-6x+5．
图象如图1．
（2）由图象可知：
①x≤1或x≥5
②∵抛物线顶点（3，-4）
∴0＜x＜5时，-4＜y₂＜5．
③由$\left\{\begin{array}{l}{y=2x+1}\\{y={x}^{2}-6x+5}\end{array}\right.$得$\left\{\begin{array}{l}{x=4+2\sqrt{3}}\\{y=9+4\sqrt{3}}\end{array}\right.或\left\{\begin{array}{l}{x=4-2\sqrt{3}}\\{y=9-4\sqrt{3}}\end{array}\right.$，
∴y₂≥y₁时，
x≤4-2$\sqrt{3}$或x≥4+2$\sqrt{3}$．
④由图象可知k＞-4．
（3）如图2，翻折后的B、C之间抛物线为y=-（x²-6x+5）=-X²+6X-5=-（x-1）（x-5），（1≤x≤5），
平移后的抛物线：y=-（x-1+n）（x-5+n），1-n＜x＜5-n，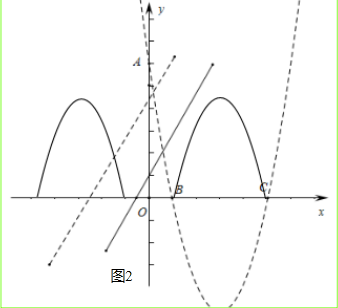
此时直线平移后的解析式为y=2x+1+n，
如果平移后的直线与平移后的二次函数相切，
则方程2x+1+n=-（x-1+n）（x-5+n）有两个相等的实数根，
即x²-（4-2n）x+n²-5n+6=0有两个相等的实数根，
△=16-16n+4n²-4n²+20n-24=0即n=2，
∵n＞2，
∴平移后的直线与平移后的抛物线不相切，
∴结合图象可知，如果平移后的直线与抛物线有公共点，
则两个临界的交点为（1-n，0），（5-n，0），
当直线y=2x+1+n经过（5-n，0）时，
0=2（5-n）+1+n，n=11，
即n的取值范围为2≤n≤11．

点评 本题考查待定系数法求二次函数的解析式、根据图象确定变量的取值范围、一次函数的性质、平移的性质、根的判别式等知识点的应用，通过做此题培养了学生的分析问题和解决问题的能力，题目综合性比较强，有一定的难度．