
【题目】已知某司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行),某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 100 | 250 | 450 |
(1)现在该公司收购了140吨蔬菜,如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工,剩余部分直接销售 |
获利(元) |
(2)如果先进行精加工,然后进行粗加工,要求15天刚好加工完140吨蔬菜,则应如何分配加工时间?
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】【发现证明】
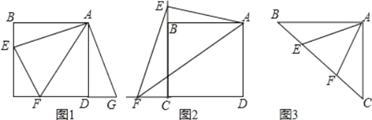
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某店购买A、B商品共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表:
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别写有数字-2,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值。放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y)。
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)若(x,y)表示平面直角坐标系中的点,求点(x,y)在函数![]() 图象上的概率。
图象上的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )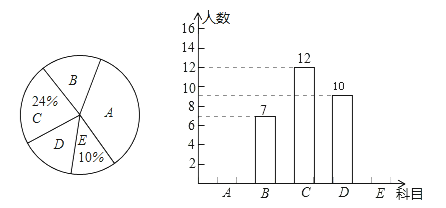
A.选科目E的有5人
B.选科目D的扇形圆心角是72°
C.选科目A的人数占体育社团人数的一半
D.选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,菱形花坛ABCD周长是80m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,相交于O点. 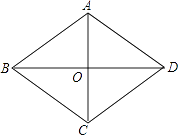
(1)求两条小路的长AC、BD.(结果可用根号表示)
(2)求花坛的面积.(结果可用根号表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com