在直角三角形ABC中，已知∠C=90°，∠A=40°，BC=3，则AC=（ ）
A.
B.
C. 
D.
科目：初中数学 来源：2014年初中毕业升学考试（浙江舟山卷）数学（解析版） 题型：选择题
一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9．这5个数据的中位数是（ ）
(A)6 (B)7 (C)8 (D)9
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（浙江温州卷）数学（解析版） 题型：选择题
如图，矩形ABCD的顶点A在第一象限，AB∥x轴，AD∥y轴，且对角线的交点与原点重合，在边AB从小于AD到大于AD的变化过程中，若矩形ABCD的周长始终保持不变，则经过动点A的反比例函数
中，k的值的变化情况是（ ）
A.一直增大 B.一直减小 C.先增大后减小 D.先减小后增大
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（浙江杭州卷）数学（解析版） 题型：填空题
设抛物线
过A(0，2)，B(4，3)，C三点，其中点C在直线
上，且点C到抛物线对称轴的距离等于1，则抛物线的函数解析式为 .
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（浙江杭州卷）数学（解析版） 题型：选择题
已知2001年至2012年杭州市小学学校数量（单位：所）和在校学生人数（单位：人）的两幅统计图，由图得出如下四个结论：
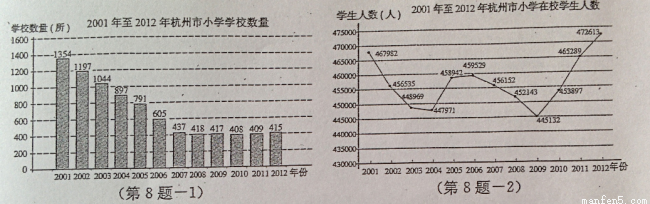
①学校数量2007至2012年比2001至2006年更稳定；
②在校学生人数有两次连续下降，两次连续增长的变化过程；
③2009年的
大于1000；
④2009~2012年，各相邻两年的学校数量增长和在校学生人数增长最快的都是2011~2012年.
其中，正确的结论是（ ）
A.①②③④ B.①②③ C.①② D.③④
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（浙江宁波卷）数学（解析版） 题型：解答题
用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。
现有19张硬纸板，裁剪时
张用A方法，其余用B方法。
（1）用
的代数式分别表示裁剪出的侧面和底面的个数；
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（浙江宁波卷）数学（解析版） 题型：填空题
为解决停车难得问题，在如图一段长56米的路段开辟停车位，每个车位是长5米、宽2.2米的矩形，矩形的边与路的边缘成45°角，那么这个路段最多可以划出 个这样的停车位（
）
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（江西南昌卷）数学（解析版） 题型：解答题
如图1，抛物线y=ax2+bx+c（a＞0）的顶点为M，直线y=m与x轴平行，且与抛物线交于点A，B，若△AMB为等腰直角三角形，我们把抛物线上A，B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形，线段AB称为碟宽，顶点M称为碟顶，点M到线段AB的距离称为碟高．
（1）抛物线y=
x2对应的碟宽为 ；抛物线y=4x2对应的碟宽为 ；抛物线y=ax2（a＞0）对应的碟宽为 ；抛物线y=a（x﹣2）2+3（a＞0）对应的碟宽为 ；
（2）抛物线y=ax2﹣4ax﹣
（a＞0）对应的碟宽为6，且在x轴上，求a的值；
（3）将抛物线y=anx2+bnx+cn（an＞0）的对应准蝶形记为Fn（n=1，2，3…），定义F1，F2，…，Fn为相似准蝶形，相应的碟宽之比即为相似比．若Fn与Fn﹣1的相似比为，且Fn的碟顶是Fn﹣1的碟宽的中点，现将（2）中求得的抛物线记为y1，其对应的准蝶形记为F1．
①求抛物线y2的表达式；
②若F1的碟高为h1，F2的碟高为h2，…Fn的碟高为hn，则hn= ，Fn的碟宽有端点横坐标为 2 ；F1，F2，…，Fn的碟宽右端点是否在一条直线上？若是，直接写出该直线的表达式；若不是，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
