
ИзНј1Ј¬ЕЧОпПЯy=ax2+bx+cЈЁaЈҫ0Ј©өД¶ҘөгОӘMЈ¬ЦұПЯy=mУлxЦбЖҪРРЈ¬ЗТУлЕЧОпПЯҪ»УЪөгAЈ¬BЈ¬ИфЎчAMBОӘөИСьЦұҪЗИэҪЗРОЈ¬ОТГЗ°СЕЧОпПЯЙПAЈ¬BБҪөгЦ®јдөДІҝ·ЦУлПЯ¶ОABО§іЙөДНјРОіЖОӘёГЕЧОпПЯ¶ФУҰөДЧјөыРОЈ¬ПЯ¶ОABіЖОӘөъҝнЈ¬¶ҘөгMіЖОӘөъ¶ҘЈ¬өгMөҪПЯ¶ОABөДҫаАліЖОӘөъёЯЈ®
ЈЁ1Ј©ЕЧОпПЯy= x2¶ФУҰөДөъҝнОӘЎЎ ЎЎЈ»ЕЧОпПЯy=4x2¶ФУҰөДөъҝнОӘЎЎ ЎЎЈ»ЕЧОпПЯy=ax2ЈЁaЈҫ0Ј©¶ФУҰөДөъҝнОӘЎЎЎЎЈ»ЕЧОпПЯy=aЈЁx©Ғ2Ј©2+3ЈЁaЈҫ0Ј©¶ФУҰөДөъҝнОӘЎЎЎЎЈ»
x2¶ФУҰөДөъҝнОӘЎЎ ЎЎЈ»ЕЧОпПЯy=4x2¶ФУҰөДөъҝнОӘЎЎ ЎЎЈ»ЕЧОпПЯy=ax2ЈЁaЈҫ0Ј©¶ФУҰөДөъҝнОӘЎЎЎЎЈ»ЕЧОпПЯy=aЈЁx©Ғ2Ј©2+3ЈЁaЈҫ0Ј©¶ФУҰөДөъҝнОӘЎЎЎЎЈ»
ЈЁ2Ј©ЕЧОпПЯy=ax2©Ғ4ax©Ғ ЈЁaЈҫ0Ј©¶ФУҰөДөъҝнОӘ6Ј¬ЗТФЪxЦбЙПЈ¬ЗуaөДЦөЈ»
ЈЁaЈҫ0Ј©¶ФУҰөДөъҝнОӘ6Ј¬ЗТФЪxЦбЙПЈ¬ЗуaөДЦөЈ»
ЈЁ3Ј©Ҫ«ЕЧОпПЯy=anx2+bnx+cnЈЁanЈҫ0Ј©өД¶ФУҰЧјөыРОјЗОӘFnЈЁn=1Ј¬2Ј¬3ЎӯЈ©Ј¬¶ЁТеF1Ј¬F2Ј¬ЎӯЈ¬FnОӘПаЛЖЧјөыРОЈ¬ПаУҰөДөъҝнЦ®ұИјҙОӘПаЛЖұИЈ®ИфFnУлFn©Ғ1өДПаЛЖұИОӘ Ј¬ЗТFnөДөъ¶ҘКЗFn©Ғ1өДөъҝнөДЦРөгЈ¬ПЦҪ«ЈЁ2Ј©ЦРЗуөГөДЕЧОпПЯјЗОӘy1Ј¬Жд¶ФУҰөДЧјөыРОјЗОӘF1Ј®
Ј¬ЗТFnөДөъ¶ҘКЗFn©Ғ1өДөъҝнөДЦРөгЈ¬ПЦҪ«ЈЁ2Ј©ЦРЗуөГөДЕЧОпПЯјЗОӘy1Ј¬Жд¶ФУҰөДЧјөыРОјЗОӘF1Ј®
ўЩЗуЕЧОпПЯy2өДұнҙпКҪЈ»
ўЪИфF1өДөъёЯОӘh1Ј¬F2өДөъёЯОӘh2Ј¬ЎӯFnөДөъёЯОӘhnЈ¬Фтhn=ЎЎЎЎЈ¬FnөДөъҝнУР¶ЛөгәбЧшұкОӘЎЎ2ЎЎЈ»F1Ј¬F2Ј¬ЎӯЈ¬FnөДөъҝнУТ¶ЛөгКЗ·сФЪТ»МхЦұПЯЙПЈҝИфКЗЈ¬ЦұҪУРҙіцёГЦұПЯөДұнҙпКҪЈ»ИфІ»КЗЈ¬ЗлЛөГчАнУЙЈ®

ЈЁ1Ј©4Ј»1Ј»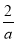 Ј»
Ј»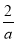 Ј®
Ј®
ЎҫҪвОцЎҝ
КФМв·ЦОцЈәЈЁ1Ј©ёщҫЭ¶ЁТеҝЙЛгіцy=ax2ЈЁaЈҫ0Ј©өДөъҝнОӘ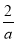 ЎўөъёЯОӘ
ЎўөъёЯОӘ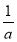 Ј¬УЙУЪЕЧОпПЯ
Ј¬УЙУЪЕЧОпПЯ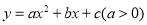 ҝЙНЁ№эЖҪТЖy=ax2ЈЁaЈҫ0Ј©өГөҪЈ¬өГөҪөъҝнОӘ
ҝЙНЁ№эЖҪТЖy=ax2ЈЁaЈҫ0Ј©өГөҪЈ¬өГөҪөъҝнОӘ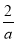 ЎўөъёЯОӘ
ЎўөъёЯОӘ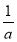 Ј¬УЙҙЛҝЙөГөъҝнЎўөъёЯЦ»УлaУР№ШЈ¬УлұрөДОЮ№ШЈ¬ҙУ¶шҝЙөГЈ®
Ј¬УЙҙЛҝЙөГөъҝнЎўөъёЯЦ»УлaУР№ШЈ¬УлұрөДОЮ№ШЈ¬ҙУ¶шҝЙөГЈ®
ЈЁ2Ј©УЙЈЁ1Ј©өДҪбВЫЈ¬ёщҫЭөъҝнТЧөГaөДЦөЈ®
ЈЁ3Ј©ўЩёщҫЭy1Ј¬ИЭТЧөГөҪy2Ј®
ўЪҪбәП»ӯНјЈ¬ТЧЦӘh1Ј¬h2Ј¬h3Ј¬ЎӯЈ¬hn©Ғ1Ј¬hn¶јФЪЦұПЯx=2ЙПЈ¬ҝЙТФҝјВЗhnЎОhn©Ғ1Ј¬ЗТ¶ј№эFn©Ғ1өДөъҝнЦРөгЈ¬Ҫш¶шҝЙөГЈ®»ӯНјКұТЧЦӘөъҝнУР№жВЙөЭјхЈ¬УЙҙЛҝЙөГУТ¶ЛөгөДМШөгЈ®¶ФУЪЎ°F1Ј¬F2Ј¬ЎӯЈ¬FnөДөъҝнУТ¶ЛөгКЗ·сФЪТ»МхЦұПЯЙПЈҝЎұЈ¬ОТГЗҝЙТФНЖІвИОТвПаБЪөДИэөгКЗ·сФЪТ»МхЦұПЯЙПЈ¬Из№ыПаБЪөДИэёцөгІ»№ІПЯФтҪбВЫІ»іЙБўЈ¬·ҙЦ®ФтіЙБўЈ¬ЛщТФҝЙТФҝјВЗ»щҙЎөДјёёцНјРО№ШПөЈ¬АыУГМШКвөгЗуЦұПЯ·ҪіМјҙҝЙЈ®
КФМвҪвОцЈәЈЁ1Ј©4Ј»1Ј»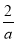 Ј»
Ј»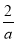 Ј®
Ј®
ЎЯaЈҫ0Ј¬
Ўаy=ax2өДНјПуҙуЦВИзПВЈә
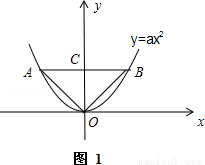
ЖдұШ№эФӯөгOЈ¬јЗABОӘЖдөъҝнЈ¬ABУлyЦбөДҪ»өгОӘCЈ¬Б¬ҪУOAЈ¬OBЈ®
ЎЯЎчDABОӘөИСьЦұҪЗИэҪЗРОЈ¬ABЎОxЦбЈ¬
ЎаOCЎНABЈ¬
ЎаЎПOCA=ЎПOCB= ЎПAOB=
ЎПAOB= ЎБ90Ўг=45ЎгЈ¬
ЎБ90Ўг=45ЎгЈ¬
ЎаЎчACOУлЎчBCOТаОӘөИСьЦұҪЗИэҪЗРОЈ¬
ЎаAC=OC=BCЈ¬
ЎаxA=-yAЈ¬xB=yBЈ¬ҙъИлy=ax2Ј¬
ЎаAЈЁ©Ғ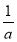 Ј¬
Ј¬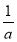 Ј©Ј¬BЈЁ
Ј©Ј¬BЈЁ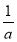 Ј¬
Ј¬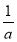 Ј©Ј¬CЈЁ0Ј¬
Ј©Ј¬CЈЁ0Ј¬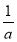 Ј©Ј¬
Ј©Ј¬
ЎаAB= Ј¬OC=
Ј¬OC=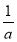 Ј¬
Ј¬
јҙy=ax2өДөъҝнОӘ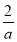 Ј®
Ј®
ўЩЕЧОпПЯy= x2¶ФУҰөДa=
x2¶ФУҰөДa= Ј¬өГөъҝн
Ј¬өГөъҝн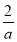 ОӘ4Ј»
ОӘ4Ј»
ўЪЕЧОпПЯy=4x2¶ФУҰөДa=4Ј¬өГөъҝнОӘ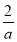 ОӘ
ОӘ Ј»
Ј»
ўЫЕЧОпПЯy=ax2ЈЁaЈҫ0Ј©Ј¬өъҝнОӘ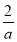 Ј»
Ј»
ўЬЕЧОпПЯy=aЈЁx©Ғ2Ј©2+3ЈЁaЈҫ0Ј©ҝЙҝҙіЙy=ax2ПтУТЖҪТЖ2ёцөҘО»іӨ¶ИЈ¬ФЩПтЙПЖҪТЖ3ёцөҘО»іӨ¶ИәуөГөҪөДНјРОЈ¬
ЎЯЖҪТЖІ»ёДұдРОЧҙЎўҙуРЎЎў·ҪПтЈ¬
ЎаЕЧОпПЯy=aЈЁx©Ғ2Ј©2+3ЈЁaЈҫ0Ј©өДЧјөъРОУлЕЧОпПЯy=ax2өДЧјөъРОИ«өИЈ¬
ЎЯЕЧОпПЯy=ax2ЈЁaЈҫ0Ј©Ј¬өъҝнОӘ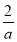 Ј¬
Ј¬
ЎаЕЧОпПЯy=aЈЁx©Ғ2Ј©2+3ЈЁaЈҫ0Ј©Ј¬өъҝнОӘ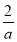 Ј®
Ј®
ЈЁ2Ј©ЎЯy=ax2©Ғ4ax©Ғ Ј¬
Ј¬
ЎаУЙЈЁ1Ј©Ј¬ЖдөъҝнОӘ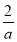 Ј¬
Ј¬
ЎЯy=ax2©Ғ4ax©Ғ өДөъҝнОӘ6Ј¬
өДөъҝнОӘ6Ј¬
Ўа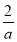 =6Ј¬
=6Ј¬
ҪвөГA=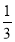 Ј¬
Ј¬
Ўаy=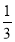 x2©Ғ
x2©Ғ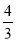 x©Ғ
x©Ғ =
=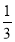 ЈЁx©Ғ2Ј©2©Ғ3
ЈЁx©Ғ2Ј©2©Ғ3
ЈЁ3Ј©ўЩЎЯF1өДөъҝнЈәF2өДөъҝн=2Јә1Ј¬
Ўа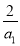 =
=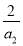 Ј¬
Ј¬
ЎЯa1=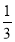 Ј¬
Ј¬
Ўаa2=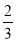 Ј®
Ј®
ЎЯy=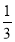 ЈЁx©Ғ2Ј©2©Ғ3өДөъҝнABФЪxЦбЙПЈЁAФЪBЧуұЯЈ©Ј¬
ЈЁx©Ғ2Ј©2©Ғ3өДөъҝнABФЪxЦбЙПЈЁAФЪBЧуұЯЈ©Ј¬
ЎаAЈЁ©Ғ1Ј¬0Ј©Ј¬BЈЁ5Ј¬0Ј©Ј¬
ЎаF2өДөъ¶ҘЧшұкОӘЈЁ2Ј¬0Ј©Ј¬
Ўаy2=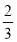 ЈЁx©Ғ2Ј©2Ј®
ЈЁx©Ғ2Ј©2Ј®
ўЪЎЯFnөДЧјөъРООӘөИСьЦұҪЗИэҪЗРОЈ¬
ЎаFnөДөъҝнОӘ2hnЈ¬
ЎЯ2hnЈә2hn©Ғ1=1Јә2Ј¬
Ўаhn=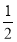 hn©Ғ1=ЈЁ
hn©Ғ1=ЈЁ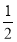 Ј©2hn©Ғ2=ЈЁ
Ј©2hn©Ғ2=ЈЁ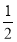 Ј©3hn©Ғ3=Ўӯ=ЈЁ
Ј©3hn©Ғ3=Ўӯ=ЈЁ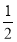 Ј©n+1h1Ј¬
Ј©n+1h1Ј¬
ЎЯh1=3Ј¬
Ўаhn=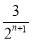 Ј®
Ј®
ЎЯhnЎОhn©Ғ1Ј¬ЗТ¶ј№эFn©Ғ1өДөъҝнЦРөгЈ¬
Ўаh1Ј¬h2Ј¬h3Ј¬ЎӯЈ¬hn©Ғ1Ј¬hn¶јФЪТ»МхЦұПЯЙПЈ¬
ЎЯh1ФЪЦұПЯx=2ЙПЈ¬
Ўаh1Ј¬h2Ј¬h3Ј¬ЎӯЈ¬hn©Ғ1Ј¬hn¶јФЪЦұПЯx=2ЙПЈ¬
ЎаFnөДөъҝнУТ¶ЛөгәбЧшұкОӘ2+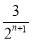 Ј®
Ј®
БнЈ¬F1Ј¬F2Ј¬ЎӯЈ¬FnөДөъҝнУТ¶ЛөгФЪТ»МхЦұПЯЙПЈ¬ЦұПЯОӘy=©Ғx+5Ј®
·ЦОцИзПВЈә
ҝјВЗFn©Ғ2Ј¬Fn©Ғ1Ј¬FnЗйРОЈ¬№ШПөИзНј2Ј¬
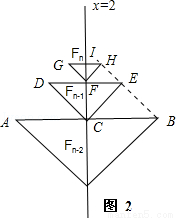
Fn©Ғ2Ј¬Fn©Ғ1Ј¬FnөДөъҝн·ЦұрОӘABЈ¬DEЈ¬GHЈ»CЈ¬FЈ¬I·ЦұрОӘЖдөъҝнөДЦРөгЈ¬¶јФЪЦұПЯx=2ЙПЈ¬Б¬ҪУУТ¶ЛөгЈ¬BEЈ¬EHЈ®
ЎЯABЎОxЦбЈ¬DEЎОxЦбЈ¬GHЎОxЦбЈ¬
ЎаABЎОDEЎОGHЈ¬
ЎаGHЖҪРРЗТөИУЪFEЈ¬DEЖҪРРЗТөИУЪCBЈ¬
ЎаЛДұЯРОGFEHЈ¬ЛДұЯРОDCBE¶јОӘЖҪРРЛДұЯРОЈ¬
ЎаHEЎОGFЈ¬EBЎОDCЈ¬
ЎЯЎПGFI= ЎПGFH=
ЎПGFH= ЎПDCE=ЎПDCFЈ¬
ЎПDCE=ЎПDCFЈ¬
ЎаGFЎОDCЈ¬
ЎаHEЎОEBЈ¬
ЎЯHEЈ¬EB¶ј№эEөгЈ¬
ЎаHEЈ¬EBФЪТ»МхЦұПЯЙПЈ¬
ЎаFn©Ғ2Ј¬Fn©Ғ1Ј¬FnөДөъҝнөДУТ¶ЛөгКЗФЪТ»МхЦұПЯЈ¬
ЎаF1Ј¬F2Ј¬ЎӯЈ¬FnөДөъҝнөДУТ¶ЛөгКЗФЪТ»МхЦұПЯЈ®
ЎЯF1Јәy1=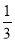 ЈЁx©Ғ2Ј©2©Ғ3ЧјөъРОУТ¶ЛөгЧшұкОӘЈЁ5Ј¬0Ј©Ј¬
ЈЁx©Ғ2Ј©2©Ғ3ЧјөъРОУТ¶ЛөгЧшұкОӘЈЁ5Ј¬0Ј©Ј¬
F2Јәy2=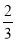 ЈЁx©Ғ2Ј©2ЧјөъРОУТ¶ЛөгЧшұкОӘЈЁ2+
ЈЁx©Ғ2Ј©2ЧјөъРОУТ¶ЛөгЧшұкОӘЈЁ2+ Ј¬
Ј¬ Ј©Ј¬
Ј©Ј¬
Ўаҙэ¶ЁПөКэҝЙөГ№эБҪөгөДЦұПЯОӘy=©Ғx+5Ј¬
ЎаF1Ј¬F2Ј¬ЎӯЈ¬FnөДөъҝнөДУТ¶ЛөгКЗФЪЦұПЯy=©Ғx+5ЙПЈ®
ҝјөгЈә1ЎўөИСьЦұҪЗИэҪЗРОЈ»2Ўў¶юҙОәҜКэөДРФЦКЈ»3¶аөг№ІПЯ


 Т»ЕөКйТөКојЩЧчТөҝмАЦјЩЖЪФЖДПГАКхіц°жЙзПөБРҙр°ё
Т»ЕөКйТөКојЩЧчТөҝмАЦјЩЖЪФЖДПГАКхіц°жЙзПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁХгҪӯОВЦЭҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәҪвҙрМв
ИзНјЈ¬ЕЧОпПЯ УлxЦбҪ»УЪAЈ¬BБҪөгЈ¬ЛьГЗөД¶ФіЖЦбУлxЦбҪ»УЪөгNЈ¬№э¶ҘөгMЧчMEЎНyЦбУЪөгEЈ¬Б¬ҪбBEҪ»MNУЪөгF.ТСЦӘөгAөДЧшұкОӘЈЁ©Ғ1Ј¬0Ј©.
УлxЦбҪ»УЪAЈ¬BБҪөгЈ¬ЛьГЗөД¶ФіЖЦбУлxЦбҪ»УЪөгNЈ¬№э¶ҘөгMЧчMEЎНyЦбУЪөгEЈ¬Б¬ҪбBEҪ»MNУЪөгF.ТСЦӘөгAөДЧшұкОӘЈЁ©Ғ1Ј¬0Ј©.
ЈЁ1Ј©ЗуёГЕЧОпПЯөДҪвОцКҪј°¶ҘөгMөДЧшұкЈ»
ЈЁ2Ј©ЗуЎчEMFУлЎчBNFөДГж»эЦ®ұИ.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁХгҪӯәјЦЭҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәСЎФсМв
ФЪЦұҪЗИэҪЗРОABCЦРЈ¬ТСЦӘЎПC=90ЎгЈ¬ЎПA=40ЎгЈ¬BC=3Ј¬ФтAC=ЈЁ Ј©
A. B.
B. C.
C.  D.
D.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁХгҪӯДюІЁҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәСЎФсМв
ТСЦӘөгAЈЁ Ј¬
Ј¬ Ј©ФЪЕЧОпПЯ
Ј©ФЪЕЧОпПЯ ЙПЈ¬ФтөгA№ШУЪЕЧОпПЯ¶ФіЖЦбөД¶ФіЖөгЧшұкОӘ
ЙПЈ¬ФтөгA№ШУЪЕЧОпПЯ¶ФіЖЦбөД¶ФіЖөгЧшұкОӘ
A. ЈЁ-3Ј¬7Ј© B. ЈЁ-1Ј¬7Ј© C. ЈЁ-4Ј¬10Ј© D. ЈЁ0Ј¬10Ј©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁХгҪӯДюІЁҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәСЎФсМв
ФІЧ¶өДДёПЯіӨОӘ4Ј¬өЧГж°лҫ¶ОӘ2Ј¬ФтҙЛФІЧ¶өДІаГж»эКЗ
A.  B.
B. 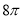 C.
C. 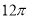 D.
D. 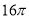
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁҪӯОчДПІэҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәҪвҙрМв
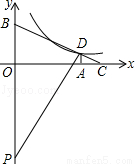
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬RtЎчPBDөДРұұЯPBВдФЪyЦбЙПЈ¬tanЎПBPD= Ј®СУіӨBDҪ»xЦбУЪөгCЈ¬№эөгDЧчDAЎНxЦбЈ¬ҙ№ЧгОӘAЈ¬OA=4Ј¬OB=3Ј®
Ј®СУіӨBDҪ»xЦбУЪөгCЈ¬№эөгDЧчDAЎНxЦбЈ¬ҙ№ЧгОӘAЈ¬OA=4Ј¬OB=3Ј®
ЈЁ1Ј©ЗуөгCөДЧшұкЈ»
ЈЁ2Ј©ИфөгDФЪ·ҙұИАэәҜКэy= ЈЁkЈҫ0Ј©өДНјПуЙПЈ¬Зу·ҙұИАэәҜКэөДҪвОцКҪЈ®
ЈЁkЈҫ0Ј©өДНјПуЙПЈ¬Зу·ҙұИАэәҜКэөДҪвОцКҪЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁҪӯОчДПІэҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
јЖЛгЈә =ЎЎ ЎЎЈ®
=ЎЎ ЎЎЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁҪӯЛХХтҪӯҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәҪвҙрМв
ИзНјЈ¬РЎГчҙУөгAіц·ўЈ¬СШЧЕЖВ¶ИОӘОӘҰБөДРұЖВПтЙПЧЯБЛ0.65З§ГЧөҪҙпөгBЈ¬sinҰБ= Ј¬И»әуУЦСШЧЕЖВ¶ИОӘi=1Јә4өДРұЖВПтЙПЧЯБЛ1З§ГЧҙпөҪөгCЈ®ОКРЎГчҙУAөгөҪөгCЙПЙэөДёЯ¶ИCDКЗ¶аЙЩЗ§ГЧЈЁҪб№ыұЈБфёщәЕЈ©Јҝ
Ј¬И»әуУЦСШЧЕЖВ¶ИОӘi=1Јә4өДРұЖВПтЙПЧЯБЛ1З§ГЧҙпөҪөгCЈ®ОКРЎГчҙУAөгөҪөгCЙПЙэөДёЯ¶ИCDКЗ¶аЙЩЗ§ГЧЈЁҪб№ыұЈБфёщәЕЈ©Јҝ

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2014ДкіхЦРұПТөЙэС§ҝјКФЈЁҪӯЛХБ¬ФЖёЫҫнЈ©КэС§ЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
Иф Ј¬
Ј¬ Ј¬Фт
Ј¬Фт өДЦөКЗ .
өДЦөКЗ .
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com