
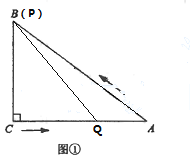
【题目】如图①,在![]() 中,
中,![]() ,
,![]() cm,动点
cm,动点![]() 以2cm/s的速度在
以2cm/s的速度在![]() 的边上沿
的边上沿![]() 的方向匀速运动,动点
的方向匀速运动,动点![]() 在
在![]() 的边上沿
的边上沿![]() 的方向匀速运动,
的方向匀速运动,![]() 、
、![]() 两点同时出发,5s后,点
两点同时出发,5s后,点![]() 到达终点
到达终点![]() ,点
,点![]() 立即停止运动(此时点
立即停止运动(此时点![]() 尚未到达点
尚未到达点![]() ).设点
).设点![]() 运动的时间为
运动的时间为![]() (s),
(s),![]() 的面积为
的面积为![]() (cm2),
(cm2),![]() 与
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)图①中![]() cm,点
cm,点![]() 运动的速度为 cm/s;
运动的速度为 cm/s;
(2)求函数![]() 的最大值;
的最大值;
(3)当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?请说明理由.
相似?请说明理由.

【答案】(1)AC=8cm,点![]() 运动的速度为5÷5=1cm/s;
运动的速度为5÷5=1cm/s;
(2)当t=4时,函数![]() 的最大值S=
的最大值S=![]()
(3) t=![]() 或t=
或t=![]()
【解析】
(1)由勾股定理求得AC的长,再利用![]() 的面积为9,得
的面积为9,得![]() ,即可解题;(2)过点P作PH⊥AC于H,证明△AHP∽△ACB得
,即可解题;(2)过点P作PH⊥AC于H,证明△AHP∽△ACB得![]() ,求出边长表示S△APQ=
,求出边长表示S△APQ=![]() =
=![]() ,整理成顶点式即可解题;(3)分两种情况讨论当∠PQA=90°时,当∠QPA=90°时,见详解.
,整理成顶点式即可解题;(3)分两种情况讨论当∠PQA=90°时,当∠QPA=90°时,见详解.
解:(1)∵动点![]() 以2cm/s的速度运动了5秒到B点, 如下图,
以2cm/s的速度运动了5秒到B点, 如下图,
∴AB=10cm,
∵![]() ,
,![]() cm,
cm,
∴AC=8cm(勾股定理)
由图2可知当时间为5秒时,![]() 的面积为9,
的面积为9,
即![]() ,
,
∵BC=CP=6,
∴AQ=3,CQ=8-3=5,
∴点![]() 运动的速度为5÷5=1cm/s;
运动的速度为5÷5=1cm/s;
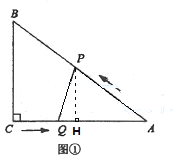
(2)如下图,过点P作PH⊥AC于H,
易证△AHP∽△ACB,
∴![]() ,
,
∴![]() ,解得:PH=
,解得:PH=![]()
∵CQ=t,
∴AQ=8-t,
∴S△APQ=![]() =
=![]() =
=![]()
∴当t=4时,函数![]() 的最大值S=
的最大值S=![]()
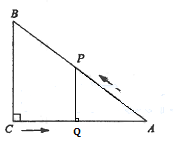
(3)分两种情况,当∠PQA=90°时,如下图,
△AQP∽△ACB,
∴![]() ,
,![]() ,解得:t=
,解得:t=![]() ;
;
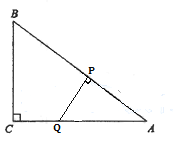
当∠QPA=90°时,如下图,
△AQP∽△ABC,
∴![]() ,
,![]() ,解得:t=
,解得:t=![]() ;
;
综上, t=![]() 或t=
或t=![]() 时以
时以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
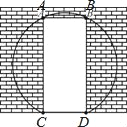
【题目】如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=![]() 米.
米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
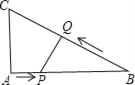
【题目】如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列各组条件,△ABC与△A1B1C1相似的有( )
①∠A=45°,AB=12,AC=15,∠A1=45°,A1B1=16,A1C1=20
②AB=12,BC=15,AC=24,A1B1=20,A1C1=40,B1C1=25
③∠B=∠B1=75°,∠C=50°,∠A1=55°
④∠C=∠C1=90°,AB=10,AC=6,A1B1=15,A1C1=9
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
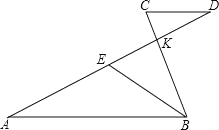
【题目】如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点,
(1)若BK=![]() KC,求
KC,求![]() 的值;
的值;
(2)联结BE,若BE平分∠ABC,则当AE=![]() AD时,猜想线段AB、BC、CD三者之间有怎样的数量关系?请写出你的结论并予以证明;
AD时,猜想线段AB、BC、CD三者之间有怎样的数量关系?请写出你的结论并予以证明;
(3)试探究:当BE平分∠ABC,且AE=![]() AD(n>2)时,线段AB、BC,CD三者之间有怎样的数量关系?请直接写出你的结论,不必证明.
AD(n>2)时,线段AB、BC,CD三者之间有怎样的数量关系?请直接写出你的结论,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
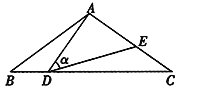
【题目】如图,在△ABC中,AB=AC=10,点D是边上一动点(不与B,C重合),∠ADE=∠B=a,DE交AC于点E,且cosa=![]() ,则线段CE的最大值为____.
,则线段CE的最大值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
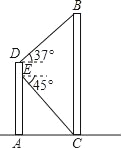
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com