

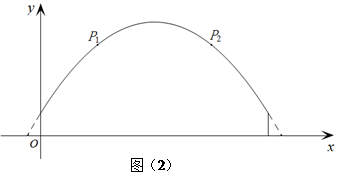
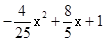 (0≤x≤10);(2)5米.
(0≤x≤10);(2)5米.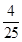
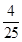 (x-5)2+5=
(x-5)2+5=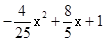 (0≤x≤10)
(0≤x≤10)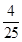 (x-5)2+5
(x-5)2+5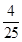 (x-5)2=1,解得x1=
(x-5)2=1,解得x1=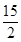 ,x2=
,x2=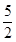


科目:初中数学 来源:不详 题型:解答题
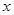 元,每售出一个小家电可获得的利润是多少元?(用含
元,每售出一个小家电可获得的利润是多少元?(用含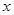 的代数式表示)
的代数式表示)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
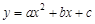 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
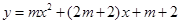 与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.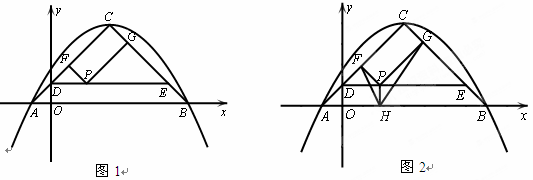
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为
的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为 (秒),
(秒), =PC2,则
=PC2,则 关于
关于 的函数图象大致为( )
的函数图象大致为( )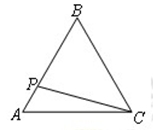

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.a>0 | B.3是方程ax²+bx+c=0的一个根 |
| C.a+b+c=0 | D.当x<1时,y随x的增大而减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com