
����Ŀ�����壺����������y1��y2���Ա���x��ȡֵ��Χ��ͬ�����Dz�����y1��y2�ı�ֵy��Ϊx�ıȺ������ұȺ������Ա���x��ȡֵ��Χ�������ı䣮���磺y1��x2+2x��x��0����y2��x��x��0������x�ıȺ���Ϊy��![]() ��x+2��x��0����
��x+2��x��0����
��1����֪y1��x2��4��2��x��3����y2��x+2��2��x��3����д��x�ıȺ���y�Ľ���ʽ�������y��ȡֵ��Χ��
��2����֪y1��x+2��x��1����y2��x��2��x��1������x�ıȺ���y��ͼ���ϵ������㣨������������궼Ϊ�����ĵ㣩�����ꣻ
��3����֪y1��x2��x+1��y2��x2+x+1����x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ��㣬��k��ȡֵ��Χ��
���𰸡���1��y��x��2��0��y��1����2�������������Ϊ��3��5������4��3������6��2������3����k��4ʱ��x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ��㣮
��������
��1�����ݱȺ����Ķ��弴�ɵó��𰸣�
��2���ȸ��ݱȺ����Ķ���д��x�ıȺ������ٽ��Ⱥ��������һ����������һ����ʽ����ʽ�����ɵó��𰸣�
��3���ȸ��ݱȺ����Ķ���д��x�ıȺ�����������Ⱥ���y��ȡֵ��Χ��������x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ������ó�x2+2x+k��ȡֵ��Χ�����ɵó���.
�⣺��1��x�ıȺ���Ϊy��![]() ��
��
��2��x��3��
��0��y��1��
��2��x�ıȺ���Ϊy��![]() ��
��
��x��1��
��x��3ʱ��y��5��x��4ʱ��y��3��x��6ʱ��y��2��
��x�ıȺ���ͼ���ϵ������������Ϊ��3��5������4��3������6��2����
��3��x�ıȺ���Ϊy��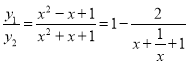 ��
��
��x��0ʱ��x+��2��
��![]() ��y��1��
��y��1��
��x��0ʱ��x+![]() ����2��
����2��
��1��y��3��
��![]() ��y��3��y��1��
��y��3��y��1��
��x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ��㣬
��x2+2x+k��3��
�ߵ�x����1ʱ�������ߵ���СֵΪk��1��
��k��1��3����k��4��
�൱k��4ʱ��x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��2![]() ��2
��2![]() ������P��ֱ��y����x���˶�����PAB��90�㣬��APB��30�㣬�ڵ�P�˶��Ĺ�����OB����СֵΪ��������
������P��ֱ��y����x���˶�����PAB��90�㣬��APB��30�㣬�ڵ�P�˶��Ĺ�����OB����СֵΪ��������
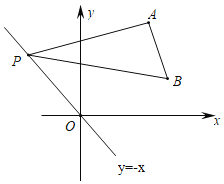
A.3.5B.2C.![]() D.2
D.2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ����֪O������ԭ�㣬B��C���������ֱ�Ϊ��3����1������2��1����

��1����O��Ϊλ��������y�����ཫ��OBC�Ŵ���������ͼ�Ρ�
��2��д��B��C����Ķ�Ӧ��B��C�����ꣻ
��3�������OBC�ڲ�һ��M������Ϊ(x��y)��д��M�Ķ�Ӧ��M�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ��Բ
��Բ![]() ��
��![]() �������ƶ�.��
�������ƶ�.��![]() �İ뾶Ϊ1����Բ��
�İ뾶Ϊ1����Բ��![]() ��
��![]() �����ܵ������������Ϊ______.
�����ܵ������������Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
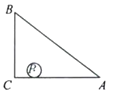
����Ŀ�����κ���y��ax2+bx+c��a��b��c�dz�����a��0��������˵����
����b2��4ac��0���������ߵĶ���һ����x���ϣ�
����b��a+c���������߱ؾ����㣨��1��0����
����a��0����һԪ���η���ax2+bx+c��0������x1��x2��x1��x2������ax2+bx+c��0�Ľ⼯Ϊx1��x��x2��
����![]() ����ax2+bx+c��0��һ��Ϊ��3��
����ax2+bx+c��0��һ��Ϊ��3��
������ȷ����_____������ȷ˵������Ŷ����ϣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
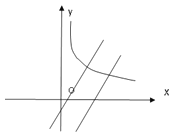
����Ŀ��ƽ��ֱ������ϵ�У�����![]() ��x>0����y=x-1��y=x-4��ͼ����ͼ��ʾ��p��a , b����ֱ��
��x>0����y=x-1��y=x-4��ͼ����ͼ��ʾ��p��a , b����ֱ��![]() ��һ���㣬���ڵ�һ����.��P��PM��x�ύֱ��
��һ���㣬���ڵ�һ����.��P��PM��x�ύֱ��![]() ��M����P��PN��y�ύ����
��M����P��PN��y�ύ����![]() ��N.
��N.
��1����PM=PNʱ����P������
��2����PM > PNʱ��ֱ��д��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
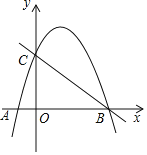
����Ŀ����ͼ����֪������y��ax2+bx+4��a��0���ĶԳ���Ϊֱ��x��3����������x���ཻ��A��B���㣬��y���ཻ�ڵ�C����֪��B������Ϊ(8��0)��
��1���������ߵĽ���ʽ��
��2����MΪ�߶�BC�Ϸ��������ϵ�һ�㣬��NΪ�߶�BC�ϵ�һ�㣬��MN��y�ᣬ��MN�����ֵ��
��3���������ߵĶԳ������Ƿ���ڵ�Qʹ�á�ACQΪ���������Σ������ڣ���ֱ��д�����ϵ�Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=8���ף�AC=16���ף���P��A��������ÿ��2�����ٶ���B�˶�����Q��Cͬʱ��������ÿ��3�����ٶ���A�˶�������һ�����㵽�˵�ʱ����һ������Ҳ��Ӧֹͣ�˶������˶���ʱ��Ϊt��
���ú�t�Ĵ���ʽ��ʾ��AP=�� ����AQ=�� ����
�Ƶ���A��P��QΪ���������������ABC����ʱ�����˶�ʱ���Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ҫ֤��ƽ���ı���ABCDΪ�����Σ���ô������Ҫ���ı���ABCD��ƽ���ı��εĻ����ϣ���һ��֤���� ��
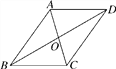
A.AB=AD��AC��BDB.AB=AD��AC=BDC.��A=��B��AC=BDD.AC��BD���ഹֱƽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com