
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0),下列说法:
①若b2﹣4ac=0,则抛物线的顶点一定在x轴上;
②若b=a+c,则抛物线必经过点(﹣1,0);
③若a<0,且一元二次方程ax2+bx+c=0有两根x1,x2(x1<x2),则ax2+bx+c<0的解集为x1<x<x2;
④若![]() ,则方程ax2+bx+c=0有一根为﹣3.
,则方程ax2+bx+c=0有一根为﹣3.
其中正确的是_____(把正确说法的序号都填上).
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日
日![]() 商用套餐正式上线.某移动营业厅为了吸引用户,设计了
商用套餐正式上线.某移动营业厅为了吸引用户,设计了![]() ,
,![]() 两个可以自由转动的转盘(如图),
两个可以自由转动的转盘(如图),![]() 转盘被等分为
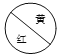
转盘被等分为![]() 个扇形,分别为红色和黄色;
个扇形,分别为红色和黄色;![]() 转盘被等分为
转盘被等分为![]() 个扇形,分别为黄色、红色、蓝色,指针固定不动.营业厅规定,每位
个扇形,分别为黄色、红色、蓝色,指针固定不动.营业厅规定,每位![]() 新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取
新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取![]() 通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形).小王办理
通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形).小王办理![]() 业务获得一次转转盘的机会,求他能免费领取
业务获得一次转转盘的机会,求他能免费领取![]() 通用流量的概率.
通用流量的概率.

A B
查看答案和解析>>
科目:初中数学 来源: 题型:
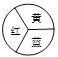
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
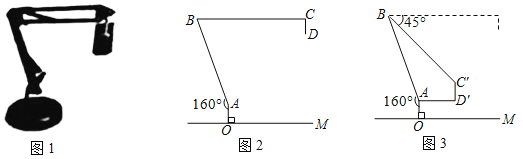
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
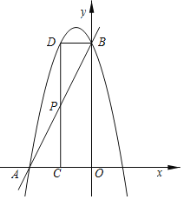
【题目】如图,已知直线y=2x+4分别交x轴,y轴于点A,B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2﹣2x+4,设其顶点为M,其对称轴交AB于点N.
①直接写出点M,N的坐标.
②若四边形MNPD为平行四边形,请求出点P的坐标.
(2)当点P的横坐标为﹣1时,是否存在这样的抛物线,使得以B,P,D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() .二次函数
.二次函数![]() 的图像经过点
的图像经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图像交于另一点
的图像交于另一点![]() .
.
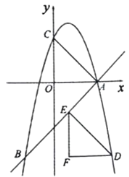
(1)求二次函数的表达式;
(2)当![]() 时,直接写出
时,直接写出![]() 的取值范围;
的取值范围;
(3)平移![]() ,使点
,使点![]() 的对应点
的对应点![]() 落在二次函数第四象限的图像上,点
落在二次函数第四象限的图像上,点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个函数y1和y2的自变量x的取值范围相同,我们不妨把y1和y2的比值y称为x的比函数,且比函数的自变量x的取值范围不发生改变.例如:y1=x2+2x(x>0),y2=x(x>0),则x的比函数为y=![]() =x+2(x>0).
=x+2(x>0).
(1)已知y1=x2﹣4(2≤x≤3),y2=x+2(2≤x≤3),写出x的比函数y的解析式,并求出y的取值范围;
(2)已知y1=x+2(x>1),y2=x﹣2(x>1),求x的比函数y的图象上的整数点(横坐标和纵坐标都为整数的点)的坐标;
(3)已知y1=x2﹣x+1,y2=x2+x+1,若x的比函数y的图象与抛物线y3=x2+2x+k(k为常数)存在交点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
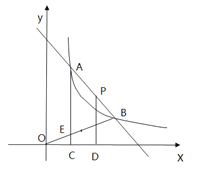
【题目】如图,一次函数y= -x+b的图象与反比例函数![]() (x>0)的图象交于点A(m , 3)和B(3 , n ).过A作AC⊥x轴于C,交OB于E,且EB = 2EO
(x>0)的图象交于点A(m , 3)和B(3 , n ).过A作AC⊥x轴于C,交OB于E,且EB = 2EO
(1)求一次函数和反比例函数解析式
(2)点P是线段AB上异于A,B的一点,过P作PD⊥x轴于D,若四边形APDC面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
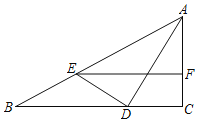
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AD交AB于E,EF∥BC交AC于F.
(1)求证:△ACD∽△ADE;
(2)求证:AD2=ABAF;
(3)作DG⊥BC交AB于G,连接FG,若FG=5,BE=8,直接写出AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0,
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根?
(2)当Rt△ABC的斜边a=![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com