
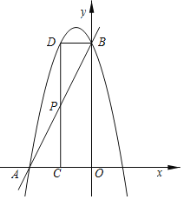
【题目】如图,已知直线y=2x+4分别交x轴,y轴于点A,B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2﹣2x+4,设其顶点为M,其对称轴交AB于点N.
①直接写出点M,N的坐标.
②若四边形MNPD为平行四边形,请求出点P的坐标.
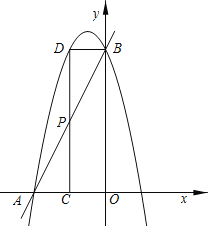
(2)当点P的横坐标为﹣1时,是否存在这样的抛物线,使得以B,P,D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
【答案】(1)①M![]() , N
, N![]() ;②P
;②P![]() ;(2)存在,y=﹣2x2﹣2x+4或y=﹣
;(2)存在,y=﹣2x2﹣2x+4或y=﹣![]() x2﹣3x+4.
x2﹣3x+4.
【解析】
(1)①抛物线的对称轴为:直线x=﹣![]() ,进而,即可求解;②PD=﹣2m2﹣2m+4﹣(2m+4)=﹣2m2﹣4m,当PD=MN时,四边形MNPD为平行四边形,即可求解;
,进而,即可求解;②PD=﹣2m2﹣2m+4﹣(2m+4)=﹣2m2﹣4m,当PD=MN时,四边形MNPD为平行四边形,即可求解;
(2)分![]() 、
、![]() 两种情况,分别求解即可.
两种情况,分别求解即可.
(1)①抛物线的对称轴为:直线x=﹣![]() ,则点M的坐标为(﹣
,则点M的坐标为(﹣![]() ,
,![]() ),
),
当x=﹣![]() 时,y=2x+4=3,
时,y=2x+4=3,
∴点N(﹣![]() ,3);
,3);
②∵M(﹣![]() ,
,![]() ),N(﹣
),N(﹣![]() ,3),
,3),
∴MN=![]() ﹣3=
﹣3=![]() .
.
设P点坐标为(m,2m+4),则D(m,﹣2m2﹣2m+4),
∴PD=﹣2m2﹣2m+4﹣(2m+4)=﹣2m2﹣4m,
∵PD∥MN,
∴当PD=MN时,四边形MNPD为平行四边形,即﹣2m2﹣4m=![]() ,
,
解得:m1=﹣![]() (舍去),m2=﹣
(舍去),m2=﹣![]() .
.
∴P点坐标为(﹣![]() ,1);
,1);
(2)存在.如图,OB=4,OA=2,则AB=![]() .
.
∵当x=﹣1时,y=2x+4=2,
∴P(﹣1,2),
∴PB=![]() .
.
设抛物线的解析式为y=ax2+bx+4,
把A(﹣2,0)代入得:4a﹣2b+4=0,解得:b=2a+2.
∴抛物线的解析式为:y=ax2+2(a+1)x+4,
∴当x=﹣1时,y=ax2+2(a+1)x+4=a﹣2a﹣2+4=2﹣a,
即:D(-1,2﹣a).
∴PD=2﹣a﹣2=﹣a,
∵DC∥OB,
∴∠DPB=∠OBA.
①当![]() 时,△PDB∽△BOA,即
时,△PDB∽△BOA,即![]() ,解得a=﹣2.
,解得a=﹣2.
此时抛物线解析式为:y=﹣2x2﹣2x+4;
②当![]() 时,△PDB∽△BAO,即
时,△PDB∽△BAO,即![]() ,解得a=﹣
,解得a=﹣![]() .
.
此时抛物线解析式为:y=﹣![]() x2﹣3x+4;
x2﹣3x+4;
综上所述,所求抛物线的解析式为:y=﹣2x2﹣2x+4或y=﹣![]() x2﹣3x+4.
x2﹣3x+4.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
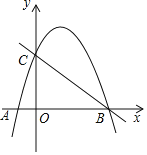
【题目】如图,反比例函数y1=![]() 与一次函数y2=ax+b的图象交于点A(﹣2,5)和点B(n,l).
与一次函数y2=ax+b的图象交于点A(﹣2,5)和点B(n,l).
(1)求反比例函数和一次函数的表达式;
(2)请结合图象直接写出当y1≥y2时自变量x的取值范围;
(3)点P是y轴上的一个动点,若S△APB=8,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0),下列说法:
①若b2﹣4ac=0,则抛物线的顶点一定在x轴上;
②若b=a+c,则抛物线必经过点(﹣1,0);
③若a<0,且一元二次方程ax2+bx+c=0有两根x1,x2(x1<x2),则ax2+bx+c<0的解集为x1<x<x2;
④若![]() ,则方程ax2+bx+c=0有一根为﹣3.
,则方程ax2+bx+c=0有一根为﹣3.
其中正确的是_____(把正确说法的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+4(a≠0)的对称轴为直线x=3,抛物线与x轴相交于A,B两点,与y轴相交于点C,已知点B的坐标为(8,0).
(1)求抛物线的解析式;
(2)点M为线段BC上方抛物线上的一点,点N为线段BC上的一点,若MN∥y轴,求MN的最大值;
(3)在抛物线的对称轴上是否存在点Q使得△ACQ为等腰三角形?若存在,请直接写出符合点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
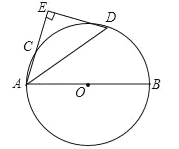
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果∠BAC=60°,AD=4,求AC长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com