
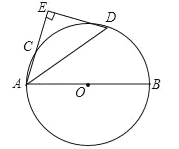
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果∠BAC=60°,AD=4,求AC长.
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,由AD为角平分线,得到一对角相等,再由OA=OD,得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行可得AE与OD平行,再由DE⊥AC,可得DE⊥OD,即DE为圆O的切线,得证;
(2)作OH⊥AC于H,则AH=CH,由已知易得四边形ODEH为矩形,从而有OH=DE=2,在Rt△OAH中, 即可求得AC的长.
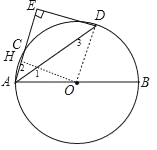
试题解析:(1)连接OD,
∵∠BAC的平分线AD交⊙O于点D,
∴∠1=∠2,
∵OA=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥AE,
∵DE⊥AE,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)作OH⊥AC于H,则AH=CH,
∵∠BAC=60°,
∴∠2=30°,
在Rt△ADE中,DE=![]() AD=2,
AD=2,
易得四边形ODEH为矩形,
∴OH=DE=2,
在Rt△OAH中,∵∠OAH=60°,
∴AH=![]() =
=![]() ,
,
∴AC=2AH=![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
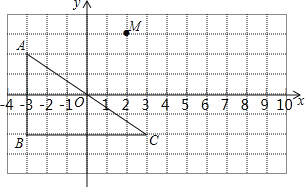
【题目】如图,已知Rt△ABC的三个顶点分别为A(-3,2),B(-3,-2),C(3,-2).将△ABC平移,使点A与点M(2,3)重合,得到△MNP.
(1)将△ABC向 平移 个单位长度,然后再向 平移 个单位长度,可以得到△MNP.
(2)画出△MNP.
(3)在(1)的平移过程中,线段AC扫过的面积为 (只需填入数值,不必写单位).
查看答案和解析>>
科目:初中数学 来源: 题型:
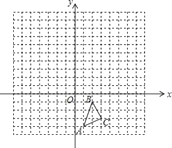
【题目】如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).
(1)以O为位似中心,作△A′B′C′∽△ABC,△A′B′C′与△ABC相似比为2:1,且△A′B′C′在第二象限;
(2)在上面所画的图形中,若线段AC上有一点D,它的横坐标为k,点D在A′C′上的对应点D′的横坐标为﹣2﹣k,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标。
的坐标。
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 横坐标比纵坐标大3;
横坐标比纵坐标大3;
(3)点![]() 在过
在过![]() 点,且与
点,且与![]() 轴平行的直线上。
轴平行的直线上。
查看答案和解析>>
科目:初中数学 来源: 题型:
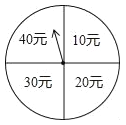
【题目】端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB、∠PCD的关系,请从你所得两个关系中选出任意一个,说明你探究的结论的正确性.

结论:(1)
(2)
选择结论: ,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
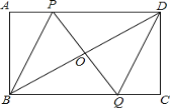
【题目】如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以![]() 的速度向点D 运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
的速度向点D 运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐家附近的商场为了吸引顾客,设立了一个可以自由转动的转盘,AB为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,顾客就可以获得相应的优惠
(1)某顾客消费40元,是否可以获得转盘的机会?
(2)某顾客正好消费66元,他转一次转盘,获得三种打折优惠的概率分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在城市改造中,市政府欲在一条人工河上架一座桥,河的两岸PQ与MN平行,河岸MN上有A、B两个相距50米的凉亭,小亮在河对岸D处测得∠ADP=60°,然后沿河岸走了110米到达C处,测得∠BCP=30°,求这条河的宽.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com